练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图1所示，点C将线段AB分成两部分，如果
    AC
    AB
    =
    BC
    AC
    ，那么点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果
    s1
    s
    =
    s2
    s1
    ，那么称直线l为该图形的黄金分割线．
    （1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点，如图2所示，则精英家教网直线CD是△ABC的黄金分割线，你认为对吗？说说你的理由；
    （2）请你说明：三角形的中线是否是该三角形的黄金分割线．
    分析：（1）结合线段的黄金分割点的概念和三角形的面积公式进行分析计算；
    （2）根据三角形的中线的概念可知分成的两个三角形的面积相等，显然不符合黄金分割线的概念．
    解答：解：∵
    S△ACD
    S△ABC
    =
    AD
    AB
    ，
    S△BCD
    S△ACD
    =
    BD
    AD
    ，
    又∵D是AB的黄金分割点，
    ∴
    AD
    AB
    =
    BD
    AD
    ，
    S△ACD
    S△ABC
    =
    S△BCD
    S△ACD
    ，
    ∴CD是△ABC的黄金分割线；

    （2）不是．
    ∵CD是△ABC的中线，
    ∴AD=DB，
    ∴
    S△ACD
    S△ABC
    =
    1
    2
    ，
    而
    S△BCD
    s△ACD
    =1，
    ∴
    S△ACD
    S△ABC
    ≠
    S△BCD
    s△ACD
    ，
    ∴中线不是黄金分割线．
    点评：主要考查的是线段的黄金分割点的概念和三角形的面积公式．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：数学教研室 题型：044

    如图(1)所示，点O是∠EPF的平分线上的一点，以O为圆心的圆和角的两边分别交于点A、B和C、D．

    求证：AB＝CD．

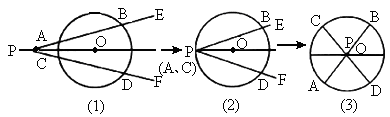
    如果将∠EPF的顶点P看成是沿着PO这条直线运动的，那么

    (1)当顶点P在⊙O上时(如图(2)所示)；是否能得到原来的结论？

    (2)当顶点P在⊙O内部时(如图(3)所示)，是否能得到原来的结论？

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    如图(1)所示，点O是∠EPF的平分线上的一点，以O为圆心的圆和角的两边分别交于点A、B和C、D．

    求证：AB＝CD．

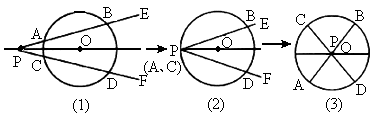
    如果将∠EPF的顶点P看成是沿着PO这条直线运动的，那么

    (1)当顶点P在⊙O上时(如图(2)所示)，是否能得到原来的结论？

    (2)当顶点P在⊙O内部时(如图(3)所示)，是否能得到原来的结论？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

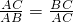    如图1所示，点C将线段AB分成两部分，如果数学公式，那么点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果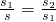数学公式，那么称直线l为该图形的黄金分割线．
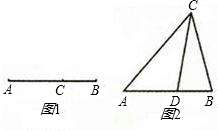    （1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点，如图2所示，则直线CD是△ABC的黄金分割线，你认为对吗？说说你的理由；
    （2）请你说明：三角形的中线是否是该三角形的黄金分割线．

    查看答案和解析>>

    科目：初中数学 来源：2009年安徽省巢湖市庐江县初中毕业班质量检测数学试卷（解析版） 题型：解答题

    （2009•庐江县模拟）如图1所示，点C将线段AB分成两部分，如果，那么点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果，那么称直线l为该图形的黄金分割线．
    （1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点，如图2所示，则直线CD是△ABC的黄金分割线，你认为对吗？说说你的理由；
    （2）请你说明：三角形的中线是否是该三角形的黄金分割线．

    查看答案和解析>>

    同步练习册答案