
”¾ĢāÄæ”æÓĆĮ½ÖÖ·½·ØÖ¤Ć÷”°Ō²µÄÄŚ½ÓĖıߊĪ¶Ō½Ē»„²¹”±£®
ŅŃÖŖ£ŗČēĶ¼¢Ł£¬ĖıߊĪABCDÄŚ½ÓÓŚ”ŃO£®
ĒóÖ¤£ŗ”ĻB£«”ĻD£½180”ć£®
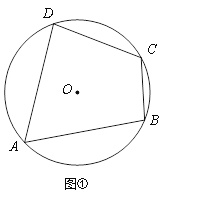

Ö¤·Ø1£ŗČēĶ¼¢Ś£¬×÷Ö±¾¶DE½»”ŃOÓŚµćE£¬Į¬½ÓAE”¢CE£®
”ßDEŹĒ”ŃOµÄÖ±¾¶£¬
”ą £®
”ß”ĻDAE£«”ĻAEC£«”ĻDCE£«”ĻADC£½360”ć£¬
”ą”ĻAEC£«”ĻADC£½360”ć£”ĻDAE£”ĻDCE£½360”ć£90”ć£90”ć£½180”ć£®
”ß”ĻBŗĶ”ĻAECĖł¶ŌµÄ»”ŹĒ![]() £¬
£¬
”ą £®
”ą”ĻB£«”ĻADC£½180”ć£®
Ēė°ŃÖ¤·Ø1²¹³äĶźÕū£¬²¢ÓĆ²»Ķ¬µÄ·½·ØĶź³ÉÖ¤·Ø2£®
Ö¤·Ø2£ŗ
”¾“š°ø”æĻź¼ū½āĪö
”¾½āĪö”æ
(1)øł¾ŻÖ±¾¶Ėł¶ŌµÄŌ²ÖܽĒĪŖ90”ć¼“æɲ¹Č«Ö¤Ć÷¹ż³Ģ£»
£Ø2£©øł¾ŻŌ²ÖܽĒÓėŌ²ŠÄ½ĒµÄ¹ŲĻµ¼°ÖܽĒĪŖ360”ć¼“æÉĒó½ā.
Ö¤·Ø1£ŗČēĶ¼¢Ś£¬×÷Ö±¾¶DE½»”ŃOÓŚµćE£¬Į¬½ÓAE”¢CE£®
”ßDEŹĒ”ŃOµÄÖ±¾¶£¬
”ą”ĻDAE£½”ĻDCE£½90”ć£®
”ß”ĻDAE£«”ĻAEC£«”ĻDCE£«”ĻADC£½360”ć£¬
”ą”ĻAEC£«”ĻADC£½360”ć£”ĻDAE£”ĻDCE£½360”ć£90”ć£90”ć£½180”ć£®
”ß”ĻBŗĶ”ĻAECĖł¶ŌµÄ»”ŹĒ![]() £¬
£¬
”ą”ĻAEC£½”ĻB£®£®
”ą”ĻB£«”ĻADC£½180”ć£®

Ö¤·Ø2£ŗĮ¬½ÓOA”¢OC
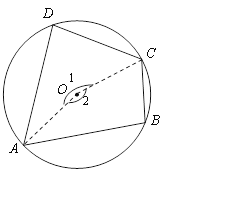
”ß”ĻB”¢”Ļ1Ėł¶ŌµÄ»”ŹĒ![]() £¬
£¬
”ĻD”¢”Ļ2Ėł¶ŌµÄ»”ŹĒ![]() £¬
£¬
”ą”ĻB£½![]() ”Ļ1£¬”ĻD£½
”Ļ1£¬”ĻD£½![]() ”Ļ2
”Ļ2
”ß”Ļ1£«”Ļ2£½360”ć£¬
”ą”ĻB£«”ĻD£½![]() (”Ļ1£«”Ļ2)£½
(”Ļ1£«”Ļ2)£½![]() ”Į360”ć£½180”ć£®
”Į360”ć£½180”ć£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=©![]() x2+mx+nÓėxÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻߵĶŌ³ĘÖį½»xÖįÓŚµćD£¬ŅŃÖŖA£Ø©1£¬0£©£¬C£Ø0£¬2£©£®
x2+mx+nÓėxÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻߵĶŌ³ĘÖį½»xÖįÓŚµćD£¬ŅŃÖŖA£Ø©1£¬0£©£¬C£Ø0£¬2£©£®
£Ø1£©ĒóÅ×ĪļĻߵıķ“ļŹ½£»
£Ø2£©ŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹”÷PCDŹĒŅŌCDĪŖŃüµÄµČŃüČż½ĒŠĪ£æČē¹ū“ęŌŚ£¬Ö±½ÓŠ“³öPµćµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©µćEŹ±Ļ߶ĪBCÉĻµÄŅ»øö¶Æµć£¬¹żµćE×÷xÖįµÄ“¹ĻßÓėÅ×ĪļĻßĻą½»ÓŚµćF£¬µ±µćEŌĖ¶Æµ½Ź²Ć“Ī»ÖĆŹ±£¬ĖıߊĪCDBFµÄĆ껿×ī“ó£æĒó³öĖıߊĪCDBFµÄ×ī“óĆ껿¼°“ĖŹ±EµćµÄ×ų±ź£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌÓŚøų¶ØŗÆŹży£½a1x2+b1x+c1£ØĘäÖŠa1”¢b1”¢c1ĪŖ³£Źż£¬ĒŅa1”Ł0£©£¬Ōņ³ĘŗÆŹży£½ £Øa1£½a2£¬b1+b2£½0£¬c1+c2£½0£©ĪŖŗÆŹży£½a1x2+b1x+c1£ØĘäÖŠa1£¬b1£¬c1ĪŖ³£Źż£¬ĒŅa1”Ł0£©µÄ”°Ļą¹ŲŗÆŹż”±£¬“Ė”°Ļą¹ŲŗÆŹż”±µÄĶ¼Ļó¼ĒĪŖG£®
£Øa1£½a2£¬b1+b2£½0£¬c1+c2£½0£©ĪŖŗÆŹży£½a1x2+b1x+c1£ØĘäÖŠa1£¬b1£¬c1ĪŖ³£Źż£¬ĒŅa1”Ł0£©µÄ”°Ļą¹ŲŗÆŹż”±£¬“Ė”°Ļą¹ŲŗÆŹż”±µÄĶ¼Ļó¼ĒĪŖG£®
£Ø1£©ŅŃÖŖŗÆŹży£½©x2+4x+2£®
¢ŁÖ±½ÓŠ“³öÕāøöŗÆŹżµÄ”°Ļą¹ŲŗÆŹż”±£»
¢ŚČōµćP£Øa£¬1£©ŌŚ”°Ļą¹ŲŗÆŹż”±µÄĶ¼ĻóÉĻ£¬ĒóaµÄÖµ£»
¢ŪČōÖ±Ļßy£½mÓėĶ¼ĻóGĒ”ŗĆÓŠĮ½øö¹«¹²µć£¬Ö±½ÓŠ“³ömµÄȔֵ·¶Ī§£»
£Ø2£©ÉčŗÆŹży£½©![]() x2+nx+1£Øn£¾0£©µÄĻą¹ŲŗÆŹżµÄĶ¼ĻóGŌŚ©4”Üx”Ü2ÉĻµÄ×īøßµćµÄׯ×ų±źĪŖy0£¬µ±
x2+nx+1£Øn£¾0£©µÄĻą¹ŲŗÆŹżµÄĶ¼ĻóGŌŚ©4”Üx”Ü2ÉĻµÄ×īøßµćµÄׯ×ų±źĪŖy0£¬µ±![]() ”Üy0”Ü9Ź±£¬Ö±½ÓŠ“³önµÄȔֵ·¶Ī§£®
”Üy0”Ü9Ź±£¬Ö±½ÓŠ“³önµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓŠĖÄÕű³ĆęĶźČ«ĻąĶ¬µÄæØʬ£¬ÕżĆęÉĻ·Ö±š±źÓŠŹż×Ö©2£¬©1£¬1£¬2£®°ŃÕāĖÄÕÅæØʬ±³Ćę³ÆÉĻ£¬Ė껜³éČ”Ņ»ÕÅ£¬¼ĒĻĀŹż×ÖĪŖm£»·Å»Ų½ĮŌČ£¬ŌŁĖ껜³éČ”Ņ»ÕÅæØʬ£¬¼ĒĻĀŹż×ÖĪŖn£¬Ōņy£½mx+n²»¾¹żµŚČżĻóĻŽµÄøÅĀŹĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼![]() ÖŠ£¬
ÖŠ£¬![]() £¬PŹĒŠ±±ßACÉĻŅ»øö¶Æµć£¬ŅŌ¼“ĪŖÖ±¾¶×÷
£¬PŹĒŠ±±ßACÉĻŅ»øö¶Æµć£¬ŅŌ¼“ĪŖÖ±¾¶×÷![]() ½»BCÓŚµćD£¬ÓėACµÄĮķŅ»øö½»µćE£¬Į¬½ÓDE£®
½»BCÓŚµćD£¬ÓėACµÄĮķŅ»øö½»µćE£¬Į¬½ÓDE£®
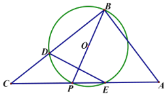
£Ø1£©µ±![]() Ź±£¬
Ź±£¬
¢ŁČō![]() £¬Ēó
£¬Ēó![]() µÄ¶ČŹż£»
µÄ¶ČŹż£»
¢ŚĒóÖ¤![]() £»
£»
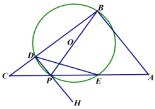
£Ø2£©µ±![]() £¬
£¬![]() Ź±£¬
Ź±£¬
¢ŁŹĒŗ¬“ęŌŚµćP£¬Ź¹µĆ![]() ŹĒµČŃüČż½ĒŠĪ£¬Čō“ęŌŚĒó³öĖłÓŠ·ūŗĻĢõ¼žµÄCPµÄ³¤£»
ŹĒµČŃüČż½ĒŠĪ£¬Čō“ęŌŚĒó³öĖłÓŠ·ūŗĻĢõ¼žµÄCPµÄ³¤£»
¢ŚŅŌDĪŖ¶Ėµć¹żP×÷ÉäĻßDH£¬×÷µćO¹ŲÓŚDEµÄ¶Ō³ĘµćQĒ”ŗĆĀäŌŚ![]() ÄŚ£¬ŌņCPµÄȔֵ·¶Ī§ĪŖ________£®£ØÖ±½ÓŠ“³ö½į¹ū£©
ÄŚ£¬ŌņCPµÄȔֵ·¶Ī§ĪŖ________£®£ØÖ±½ÓŠ“³ö½į¹ū£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖÅäŗĻČ«ŹŠ”°½ūÖ¹·ŁÉÕ½ÕøŃ”±¹¤×÷£¬Ä³Ń§Š£¾ŁŠŠĮĖ”°½ūÖ¹·ŁÉÕ½ÕøŃ£¬±£»¤»·¾³£¬“ÓĪŅ×öĘš”±ĪŖÖ÷ĢāµÄŃŻ½²±ČČü. Čüŗó×éĪÆ»įÕūĄķ²ĪČüĶ¬Ń§µÄ³É¼Ø£¬²¢ÖĘ×÷ĮĖČēĻĀ²»ĶźÕūµÄʵŹż·Ö²¼±ķŗĶʵŹż·Ö²¼Ö±·½Ķ¼£¬Ēėøł¾ŻĶ¼±ķĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
·ÖŹż¶Ī £Ø·ÖŹżĪŖx·Ö£© | ʵŹż | °Ł·Ö±Č |
60”Üx£¼70 | 8 | 20% |
70”Üx£¼80 | a | 30% |
80”Üx£¼90 | 16 | b% |
90”Üx£¼100 | 4 | 10% |
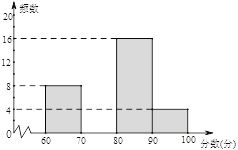
£Ø1£©±ķÖŠµÄa£½ £¬b£½””””””””””£»
£Ø2£©Ēė²¹Č«ĘµŹż·Ö²¼Ö±·½Ķ¼£»
£Ø3£©ČōÓĆÉČŠĪĶ³¼ĘĶ¼Ą“ĆčŹö³É¼Ø·Ö²¼Ēéæö£¬Ōņ·ÖŹż¶Ī70”Üx£¼80¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹżŹĒ £»
£Ø4£©¾ŗČü³É¼Ø²»µĶÓŚ90·ÖµÄ4ĆūĶ¬Ń§ÖŠÕżŗĆÓŠ2ĆūÄŠĶ¬Ń§£¬2ĆūÅ®Ķ¬Ń§.ѧŠ£“ÓÕā4ĆūĶ¬Ń§ÖŠĖ껜³éČ”2ĆūĶ¬Ń§½ÓŹÜµēŹÓĢؼĒÕß²É·Ć£¬ĒėÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·ØĒóÕżŗĆ³éµ½Ņ»ĆūÄŠĶ¬Ń§ŗĶŅ»ĆūÅ®Ķ¬Ń§µÄøÅĀŹ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£Ø1£©£¬AB=CD£¬AD=BC£¬OĪŖACÖŠµć£¬¹żOµćµÄÖ±Ļß·Ö±šÓėAD”¢BCĻą½»ÓŚµćM”¢N£¬ÄĒĆ“”Ļ1Óė”Ļ2ÓŠŹ²Ć“¹ŲĻµ£æĒėĖµĆ÷ĄķÓÉ£»
Čō¹żOµćµÄÖ±Ļߊż×ŖÖĮĶ¼£Ø2£©”¢£Ø3£©µÄĒéæö£¬ĘäÓąĢõ¼ž²»±ä£¬ÄĒĆ“Ķ¼£Ø1£©ÖŠµÄ”Ļ1Óė”Ļ2µÄ¹ŲĻµ³ÉĮ¢Āš£æĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢĘ·ĻÖŌŚµÄŹŪ¼ŪĪŖĆ漞60ŌŖ£¬ĆæŠĒĘŚæÉĀō³ö300¼ž. ŹŠ³”µ÷²é·“Ó³£ŗČēµ÷Õū¼Ūøń£¬Ćæ½µ¼Ū1ŌŖ£¬ĆæŠĒĘŚæɶąĀō³ö20¼ž. ŅŃÖŖÉĢĘ·µÄ½ų¼ŪĪŖĆ漞40ŌŖ£¬ČēŗĪ¶Ø¼Ū²ÅÄÜŹ¹ĄūČó×ī“ó£æÕāøö×ī“óĄūČóŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij×ŌŠŠ³µ¾ĻśÉĢ¼Ę»®Ķ¶Čė7.1ĶņŌŖ¹ŗ½ų100Į¾AŠĶŗĶ30Į¾BŠĶ×ŌŠŠ³µ£¬ĘäÖŠBŠĶ³µµ„¼ŪŹĒAŠĶ³µµ„¼ŪµÄ6±¶ÉŁ60ŌŖ£®
£Ø1£©ĒóA”¢BĮ½ÖÖŠĶŗŵÄ×ŌŠŠ³µµ„¼Ū·Ö±šŹĒ¶ąÉŁŌŖ£æ
£Ø2£©ŗóĄ“ÓÉÓŚøĆ¾ĻśÉĢ׏½š½ōÕÅ£¬Ķ¶Čė¹ŗ³µµÄ׏½š²»³¬¹ż5.86ĶņŌŖ£¬µ«¹ŗ½ųÕāÅś×ŌŠŠÄźµÄ×ÜŹż²»±ä£¬ÄĒĆ“ÖĮ¶ąÄܹŗ½ųBŠĶ³µ¶ąÉŁĮ¾£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com