
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据相似三角形的判定定理:三条对应边的比相等的三角形相似可得需①②组合,对应边成比例且夹角相等的三角形相似可得②④组合,有两角对应相等的三角形相似可得③④组合,则可求得答案.
解答 解:①②组合,
∵$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$,$\frac{BC}{B′C′}$=$\frac{AC}{A′C′}$,
∴$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$=$\frac{AC}{A′C′}$;
∴△ABC∽△A′B′C′(三条对应边的比相等的三角形相似);
②④组合,
∵$\frac{BC}{B′C′}$=$\frac{AC}{A′C′}$,∠C=∠C′,
∴△ABC∽△A′B′C′(对应边成比例且夹角相等的三角形相似);
③④组合,
∵∠A=∠A′,∠C=∠C′,
∴△ABC∽△A′B′C′(有两角对应相等的三角形相似).
∴能判断△ABC∽△A′B′C′的共有3组.
故选C.
点评 此题考查了相似三角形的判定.此题难度不大,解题的关键是熟记相似三角形的判定定理,掌握定理的应用.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
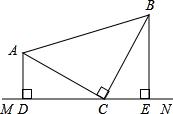 如图,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN,BE⊥MN,垂足分别为点D,E.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN,BE⊥MN,垂足分别为点D,E.求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AC=A'C',BC=B'C' | B. | AB=A'B',AC=A'C' | C. | AB=B'C',AC=A'C' | D. | ∠B=∠B',AB=A'B' |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com