
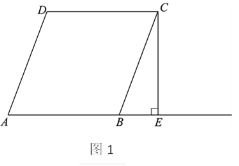
【题目】如图,在菱形ABCD中,CE⊥AB交AB延长线于点E,点F为点B关于CE的对称点,连接CF,分别延长DC,CF至点G,H,使FH=CG,连接AG,DH交于点P.
(1)依题意补全图1;
(2)猜想AG和DH的数量关系并证明;
(3)若∠DAB=70°,是否存在点G,使得△ADP为等边三角形?若存在,求出CG的长;若不存在,说明理由.
【答案】(1)见解析;(2) AG=DH,理由见解析;(3) 不存在.理由见解析.
【解析】(1)依题意画图;
(2)根据菱形性质得![]() ,
,![]() ∥
∥![]() ,
,![]() ;由点
;由点![]() 为点
为点![]() 关于
关于![]() 的对称点,得
的对称点,得![]() 垂直平分
垂直平分![]() ,故
,故![]() ,
,![]() ,所以
,所以![]() ,再证
,再证![]() ,
,
由![]() ,
,![]() ,得
,得![]() .可证△
.可证△![]() ≌△
≌△![]() .
.
(3)由(2)可知,∠DAG=∠CDH,∠G=∠GAB,
证得∠DPA=∠PDG+∠G=∠DAG+∠GAB=70°>60°,故△ADP不可能是等边三角形.
(1)补全的图形,如图所示.

(2)AG=DH.
证明:∵四边形ABCD是菱形,
∴![]() ,
,![]() ∥
∥![]() ,
,![]() .
.
∵点![]() 为点
为点![]() 关于
关于![]() 的对称点,
的对称点,
∴![]() 垂直平分
垂直平分![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴△![]() ≌△
≌△![]() .
.
∴![]() .
.
(3)不存在.
理由如下:
由(2)可知,∠DAG=∠CDH,∠G=∠GAB,
∴∠DPA=∠PDG+∠G=∠DAG+∠GAB=70°>60°.
∴△ADP不可能是等边三角形.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
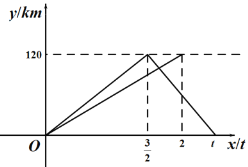
【题目】一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的1.5倍,往返共用t小时.一辆货车同时从甲地驶往乙地,到达乙地后停止.两车同时出发,匀速行驶,设轿车行驶的时间为x(h),两车离开甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图所示.
(1)轿车从乙地返回甲地的速度为 km/t,t= h;
(2)求轿车从乙地返回甲地时y与x之间的函数关系式;
(3)当轿车从甲地返回乙地的途中与货车相遇时,求相遇处到甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6min发现忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前走,小亮取回借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆。已知骑车的速度是步行速度的2倍,如图是小亮和姐姐距离家的路程y(m)与出发的时间x(min)的函数图象,根据图象解答下列问题:
(1)小亮在家停留了多长时间?
(2)求小亮骑车从家出发去图书馆时距家的路程 y(m)与出发时间 x(min)之间的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
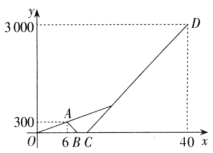
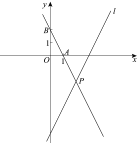
【题目】如图,在平面直角坐标系xOy中,直线![]() 的表达式为
的表达式为![]() ,点A,B的坐标分别为
,点A,B的坐标分别为
(1,0),(0,2),直线AB与直线![]() 相交于点P.
相交于点P.
(1)求直线AB的表达式;
(2)求点P的坐标;
(3)若直线![]() 上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一束光线与水平面成60°的角度照射地面,现在地面AB上支放一个平面镜CD,使这束光线经过平面镜反射后成水平光线,则平面镜CD与地面AB所成角∠DCB的度数等于( ) 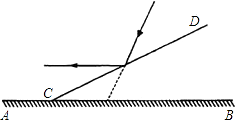
A.30°
B.45°
C.50°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=--![]() x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
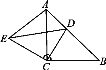
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
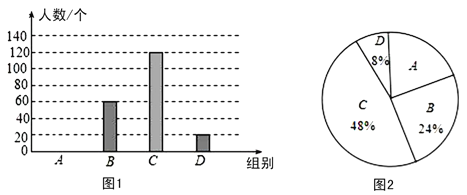
根据以上信息,回答下列问题:
(1)A组的人数是 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 ;
(3)根据统计数据估计该地区25 000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.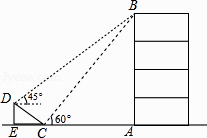
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com