


 ,b=2,
,b=2, x+2,
x+2,
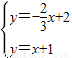
 .
. 小时甲、乙两个蓄水池中水的深度相同;
小时甲、乙两个蓄水池中水的深度相同; t+2)=S2(t+1)
t+2)=S2(t+1)

科目:初中数学 来源:2005年全国中考数学试题汇编《一次函数》(05)(解析版) 题型:解答题
 ,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.
,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《一次函数》(05)(解析版) 题型:解答题
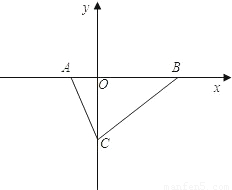 轴上,tan∠ABC=
轴上,tan∠ABC= ,点P在线段OC上,且PO、PC的长(PO<PC)是方程x2-12x+27=0的两根.
,点P在线段OC上,且PO、PC的长(PO<PC)是方程x2-12x+27=0的两根.查看答案和解析>>
科目:初中数学 来源:2010年中考数学考前10日信息题复习题精选(1)(解析版) 题型:解答题
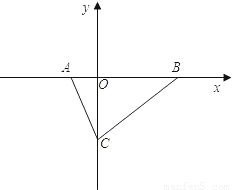 轴上,tan∠ABC=
轴上,tan∠ABC= ,点P在线段OC上,且PO、PC的长(PO<PC)是方程x2-12x+27=0的两根.
,点P在线段OC上,且PO、PC的长(PO<PC)是方程x2-12x+27=0的两根.查看答案和解析>>
科目:初中数学 来源:2005年黑龙江省中考数学试卷(课标卷)(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2005年黑龙江省中考数学试卷(大纲卷)(解析版) 题型:解答题
 ,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.
,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com