
【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次,平均数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
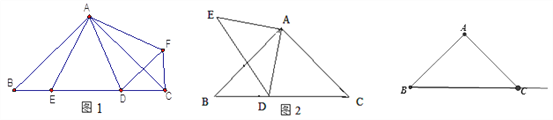
【题目】(1)如图1,在Rt△ABC 中, ![]() ,D、E是斜边BC上两动点,且∠DAE=45°,将△
,D、E是斜边BC上两动点,且∠DAE=45°,将△![]() 绕点
绕点![]() 逆时针旋转90后,得到△
逆时针旋转90后,得到△![]() ,连接
,连接![]() .
.
(1)试说明:△![]() ≌△
≌△![]() ;
;
(2)当BE=3,CE=9时,求∠BCF的度数和DE的长;
(3)如图2,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,D是斜边BC所在直线上一点,BD=3,BC=8,求DE2的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某开发区综合治理指挥部决定购买A、B两种型号的污水处理设备共10台(注:要求同时有两种型号),买2台A型设备和3台B型设备共需要90万元,其中A型设备单价是B型设备单价的1.5倍;经预算,指挥部购买污水处理设备经费不超过180万元,请解答下列问题
(1)A型设备和B型设备的单价各是多少万元?
(2)指挥部有哪几种购买方案?
(3)若A型设备月处理污水量200吨、B型设各月处理污水量180吨,现要求月处理污水量不低于1840吨,设购买设备需要总费用为y万元,A型设备x台,请写出y与x的函数解析式,并根据函数性质选择更省钱的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了预测本校九年级男生毕业体育测试达标情况,随机抽取该年级部分男生进行一次测试(满分50分,成绩均记为整数分),并按测试成绩m(单位:分)分类:A类(45<m≤50),B类(40<m≤45),C类(35<m≤40),D类(m≤35)绘制出如图所示的不完整条形统计图,请根据图中信息解答下列问题:
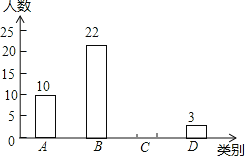
(1)a= ,b= ,c= ;
成绩等级 | 人数 | 所占百分比 |
A类(45 | 10 | 20% |
B类 | 22 | 44% |
C类 | a | b |
D类 | c |
(2)补全条形统计图;
(3)若该校九年级男生有600名,D类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD,点E是BC边上的一点,将边AD延长至点F,使∠AFC=∠DEC.

(1)求证:四边形DECF是平行四边形;
(2)若AB=13,DF=14,tan A=![]() ,求CF的长.
,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
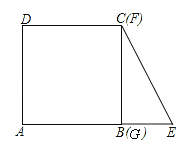
【题目】如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的
一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运
动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为
A.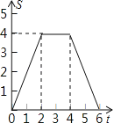 B.
B.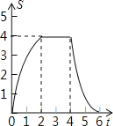
C.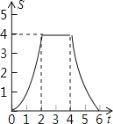 D.
D.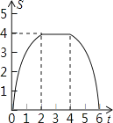
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务.
三等分任意角问题是数学史上一个著名的问题,直到1837年,数学家才证明了“三等分任意角”是不能用尺规完成的.
在探索中,出现了不同的解决问题的方法
方法一:
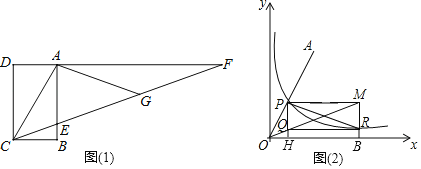
如图(1),四边形ABCD是矩形,F是DA延长线上一点,G是CF上一点,CF与AB交于点E,且∠ACG=∠AGC,∠GAF=∠F,此时∠ECB=![]() ∠ACB.
∠ACB.
方法二:
数学家帕普斯借助函数给出一种“三等分锐角”的方法(如图(2)):将给定的锐角∠AOB置于平面直角坐标系中,边OB在x轴上,边OA与函数y=![]() 的图象交于点P,以点P为圆心,以2OP长为半径作弧交图象于点R.过点P作x轴的平行线,过点R作y轴的平行线,两直线相交于点M,连接OM得到∠AOB,过点P作PH⊥x轴于点H,过点R作RQ⊥PH于点Q,则∠MOB=
的图象交于点P,以点P为圆心,以2OP长为半径作弧交图象于点R.过点P作x轴的平行线,过点R作y轴的平行线,两直线相交于点M,连接OM得到∠AOB,过点P作PH⊥x轴于点H,过点R作RQ⊥PH于点Q,则∠MOB=![]() ∠AOB.
∠AOB.
(1)在“方法一”中,若∠ACF=40°,GF=4,求BC的长.
(2)完成“方法二”的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时.数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速在l外取一点P,作PC⊥1,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°,测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速?(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
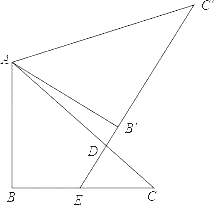
【题目】如图,在Rt△ABC中,∠ABC=90°,![]() .将△ABC绕点A逆时针旋转60°,得到△AB'C'(点B,C的对应点分别为点B′,C′),延长C′B′分别交AC,BC于点D,E,若DE=2,则AD的长为_____.
.将△ABC绕点A逆时针旋转60°,得到△AB'C'(点B,C的对应点分别为点B′,C′),延长C′B′分别交AC,BC于点D,E,若DE=2,则AD的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com