
【题目】如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.

(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)若点N是抛物线上的动点,过点N作NH⊥x轴,垂足为H,以B,N,H为顶点的三角形是否能够与△OBC相似(排除全等的情况)?若能,请求出所有符合条件的点N的坐标;若不能,请说明理由.
【答案】(1)y=![]() x2-
x2-![]() x+2;(2)直线BC的解析式y=-
x+2;(2)直线BC的解析式y=-![]() x+2;(3)N点的坐标为(5,2)、(2,-1)或(-3,14).
x+2;(3)N点的坐标为(5,2)、(2,-1)或(-3,14).
【解析】
试题分析:(1)把点A坐标代入抛物线y=ax2-5ax+2(a≠0)求得抛物线的解析式即可;
(2)求出抛物线的对称轴,再求得点B、C坐标,设直线BC的解析式为y=kx+b,再把B、C两点坐标代入线BC的解析式为y=kx+b,求得k和b即可;
(3)设N(x,ax2-5ax+2),分两种情况讨论:①△OBC∽△HNB,②△OBC∽△HBN,根据相似,得出比例式,再分别求得点N坐标即可.
试题解析:(1)∵点A(1,0)在抛物线y=ax2-5ax+2(a≠0)上,
∴a-5a+2=0,
∴a=![]() ,
,
∴抛物线的解析式为y=![]() x2-
x2-![]() x+2;
x+2;
(2)抛物线的对称轴为直线x=![]() ,
,
∴点B(4,0),C(0,2),
设直线BC的解析式为y=kx+b,
∴把B、C两点坐标代入线BC的解析式为y=kx+b,得
![]() ,
,
解得k=-![]() ,b=2,
,b=2,
∴直线BC的解析式y=-![]() x+2;
x+2;
(3)设N(x,![]() x2-
x2-![]() x+2),分三种情况讨论:
x+2),分三种情况讨论:
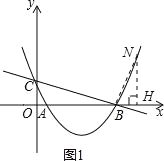
①当△OBC∽△HNB时,如图1,
![]() ,
,
即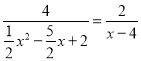 ,
,
解得x1=5,x2=4(不合题意,舍去),
∴点N坐标(5,2);
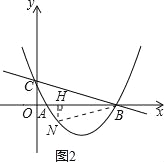
②当△OBC∽△HBN时,如图2,
![]() ,
,
即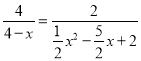 ,
,
解得x1=2,x2=4(不合题意舍去),
∴点N坐标(2,-1);
③当N(x,![]() x2-
x2-![]() x+2)在第二象限时,
x+2)在第二象限时,
H(x,0)在x轴的负半轴上,
∴BH=4-x,
∵△OBC∽△HNB,
∴![]() ,
,
即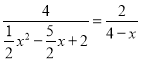 ,
,
得到x2-x-12=0
解得x1=4(舍去);x2=-3,
∴N点的坐标为(-3,14)
综上所述,N点的坐标为(5,2)、(2,-1)或(-3,14),使得以点B、N、H为顶点的三角形与△OBC相似.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,正确的是( )
A. 对角线相等的平行四边形是菱形
B. 有两边及一角相等的两个三角形全等
C. 同位角相等
D. 直角三角形斜边上的中线等于斜边的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是 [ ]
A. 几个有理数相乘,当因数有奇数个时,积为负
B. 几个有理数相乘,当正因数有奇数个时,积为负
C. 几个有理数相乘,当积为负数时,负因数有奇数个
D. 几个有理数相乘,当负因数有偶数个时,积为负
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com