
【题目】如图1,![]() 内接于⊙O,过C作射线CP与BA的延长线交于点P,
内接于⊙O,过C作射线CP与BA的延长线交于点P,![]() .
.

(1)求证:CP是⊙O的切线;
(2)若![]() ,
,![]() ,求AB的长;
,求AB的长;
(3)如图2,D是BC的中点,PD与AC交于点E,求证:![]() .
.
科目:初中数学 来源: 题型:
【题目】“五一”小长假期间,小李一家想到以下四个5A级风景区旅游:A.石林风景区;B.香格里拉普达措国家公园;C.腾冲火山地质公园;D.玉龙雪山景区.但因为时间短,小李一家只能选择其中两个景区游玩
(1)若小李从四个景区中随机抽出两个景区,请用树状图或列表法求出所有可能的结果;
(2)在随机抽出的两个景区中,求抽到玉龙雪山风景区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
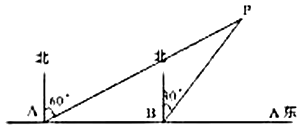
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=120°,AC=2,⊙O是△ABC的外接圆,D是![]() 上任意一点(不包括点A、C),顺次连接四边形ABCD四边中点得到四边形EFGH,则四边形EFGH的周长的最大值为____________.
上任意一点(不包括点A、C),顺次连接四边形ABCD四边中点得到四边形EFGH,则四边形EFGH的周长的最大值为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(概念提出)如图 ①,若正△DEF的三个顶点分别在正△ABC的边AB、BC、AC上,则我们称△DEF是正△ABC的内接正三角形.
(1)求证:△ADF≌△BED.
(问题解决)利用直尺和圆规作正三角形的内接正三角形(保留作图痕迹,不写作法).
(2)如图 ②,正△ABC的边长为a,作正△ABC的内接正△DEF,使△DEF的边长最短,并说明理由;
(3)如图③,作正△ABC的内接正△DEF,使FD⊥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】女本柔弱,为母则刚,说的是母亲对子女无私的爱,母爱伟大,值此母亲节来临之际,某花店推出一款康乃馨花束,经过近几年的市场调研发现,该花束在母亲节的销售量![]() (束)与销售单价
(束)与销售单价![]() (元)之间满足如图所示的一次函数关系,已知该花束的成本是每束100元.
(元)之间满足如图所示的一次函数关系,已知该花束的成本是每束100元.
(1)求出![]() 关于
关于![]() 的函数关系式(不要求写
的函数关系式(不要求写![]() 的取值范围);
的取值范围);
(2)设该花束在母亲节盈利为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式:并求出当售价定为多少元时,利润最大?最大值是多少?
的函数关系式:并求出当售价定为多少元时,利润最大?最大值是多少?
(3)花店开拓新的进货渠道,以降低成本.预计在今后的销售中,母亲节期间该花束的销售量与销售单价仍存在(1)中的关系.若想实现销售单价为200元,且销售利润不低于9900元的销售目标,该花束每束的成本应不超过多少元.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴相交于点A(﹣1,0)、B(5,0),与y轴相交于点C(0,![]() ).
).
(1)求该函数的表达式;
(2)设E为对称轴上一点,连接AE、CE;
①当AE+CE取得最小值时,点E的坐标为 ;
②点P从点A出发,先以1个单位长度/的速度沿线段AE到达点E,再以2个单位长度的速度沿对称轴到达顶点D.当点P到达顶点D所用时间最短时,求出点E的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com