
分析 (1)首先提取公因式a,进而利用平方差公式分解因式得出答案;
(2)直接提取公因式4(x-y),进而分解因式得出答案;
(3)首先利用平方差公式分解因式,再利用完全平方公式分解因式;
(4)首先去括号,合并同类项,再利用完全平方公式分解因式得出答案.
解答 解:(1)a3-4a=a(a2-4)=a(a+2)(a-2);
(2)4a(x-y)+8b(y-x)=4(x-y)(a-2b);
(3)(a2+4)2-16a2
=(a2+4-4a)(a2+4+4a)
=(a-2)2(a+2)2;
(4)(x+4)(x+6)+1
=x2+10x+24+1
=x2+10x+25
=(x+5)2.
点评 此题主要考查了提取公因式法以及公式法分解因式,正确应用公式法分解因式是解题关键.


科目:初中数学 来源: 题型:填空题
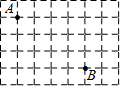 如图,长方形网格由小正方形构成,每一个小正方形的边长都为1,点A和点B是小正方形的格点,请你在图中画出从A到B的最短路程,则点A和点B之间的这个最短路程值为5.
如图,长方形网格由小正方形构成,每一个小正方形的边长都为1,点A和点B是小正方形的格点,请你在图中画出从A到B的最短路程,则点A和点B之间的这个最短路程值为5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
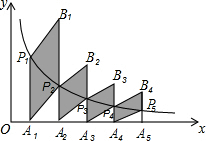 如图,分别过反比例函数y=$\frac{3}{x}$图象上的点P1(1,y1),P2(2,y2),…,Pn(n,yn)作x轴的垂线,垂足分别为A1,A2,…,An,连接A1P2,A2P3,…,AnPn+1,…,以A1P1,A1P2为一组邻边作平行四边形A1P1B1P2,其面积为S1,以A2P2,A2P3为一组邻边作平行四边形A2P2B2P3,其面积为S2,…,以AnPn,AnPn+1为一组邻边作平行四边形AnPnBnPn+1,其面积为Sn,若S1+S2+…+Sn>8,则n的最小值为( )
如图,分别过反比例函数y=$\frac{3}{x}$图象上的点P1(1,y1),P2(2,y2),…,Pn(n,yn)作x轴的垂线,垂足分别为A1,A2,…,An,连接A1P2,A2P3,…,AnPn+1,…,以A1P1,A1P2为一组邻边作平行四边形A1P1B1P2,其面积为S1,以A2P2,A2P3为一组邻边作平行四边形A2P2B2P3,其面积为S2,…,以AnPn,AnPn+1为一组邻边作平行四边形AnPnBnPn+1,其面积为Sn,若S1+S2+…+Sn>8,则n的最小值为( )| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com