
分析 在Rt△AOB中,可求得OA、OB,则可求得AC和BD的长,利用菱形的面积公式可求得答案.
解答 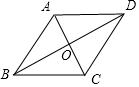 解:
解:
∵四边形ABCD为菱形,
∴AB∥CD,AC⊥BD,AO=OC,BO=OD,
∴∠ABO=∠BDC=30°,
∵AB=8,
∴AO=$\frac{1}{2}$AB=4,BO=$\frac{\sqrt{3}}{2}$AB=4$\sqrt{3}$,
∴AC=2AO=8,BD=2BO=8$\sqrt{3}$,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×8×8$\sqrt{3}$=32$\sqrt{3}$,
故答案为:32$\sqrt{3}$.
点评 本题主要考查菱形的性质,利用条件求得菱形的对角线是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
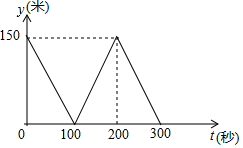 一次越野跑中,小明和小刚同时出发,当小明跑了1600米时,小刚跑的1400米,此后两人分别以a米/秒、b米/秒的速度匀速跑,他们之间的距离y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为1800米.
一次越野跑中,小明和小刚同时出发,当小明跑了1600米时,小刚跑的1400米,此后两人分别以a米/秒、b米/秒的速度匀速跑,他们之间的距离y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为1800米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com