
【题目】如图,等腰三角形ABC的底边BC长为6,面积是18,腰AB的垂直平分线EF分別交AC、AB边于E、F点.若点O为BC边的中点,点M为线段EF上一动点,则△BOM周长的最小值为_______.

【答案】9
【解析】
连接AO,AM.由于△ABC是等腰三角形,点O是BC边的中点,故AO⊥BC,再根据三角形的面积公式求出AO的长,再再根据EF是线段AB的垂直平分线可知,点B关于直线EF的对称点为点A,由OM+BM=OM+AM≥OA,可知AO的长为BM+MO的最小值,由此即可解决问题;
连接AO,AM.

∵△ABC是等腰三角形,点O是BC边的中点,
∴AO⊥BC,
∴S△ABC=![]() BCAO=
BCAO=![]() ×6×AO=18,
×6×AO=18,
解得AO=6,
∵EF是线段AC的垂直平分线,
∴点CB于直线EF的对称点为点A,
∴BM=MA,
∵OM+BM=OM+AM≥OA,
∴AO的长为BM+MO的最小值,
∴△BOM的周长最小值=(BM+MO)+BO=AO+![]() BC=6+
BC=6+![]() ×6=6+3=9.
×6=6+3=9.
故答案为:9.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO. 
(1)已知BD= ![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等腰直角三角形,D为斜边AB上任意一点,(不与点A、B重合),连接CD,作EC⊥DC,且EC=DC,连接AE,则∠EAC为_______________度.
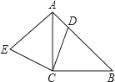
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AD平分∠CAE,AD∥BC.
(1)求证:△ABC是等腰三角形.
(2)当∠CAE等于多少度时△ABC是等边三角形?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在关于x的分式方程 ![]() ①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
(1)求k的取值范围;
(2)当方程②有两个整数根x1、x2 , k为整数,且k=m+2,n=1时,求方程②的整数根;
(3)当方程②有两个实数根x1、x2 , 满足x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),且k为负整数时,试判断|m|≤2是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:a1= ![]() =
= ![]() ﹣1,
﹣1,
第2个等式:a2= ![]() =
= ![]() ﹣
﹣ ![]() ,
,
第3个等式:a3= ![]() =2﹣
=2﹣ ![]() ,
,
第4个等式:a4= ![]() =
= ![]() ﹣2,
﹣2,
按上述规律,回答以下问题:
(1)请写出第n个等式:an=;
(2)a1+a2+a3+…+an= .
查看答案和解析>>
科目:初中数学 来源: 题型:
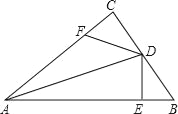
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与抛物线y= ![]() x2交于A(x1 , y1)、B(x2 , y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为 .
x2交于A(x1 , y1)、B(x2 , y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,∠B=∠C=90 ,M是BC的中点,DM平分∠ADC.
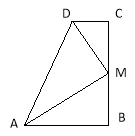
(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;
(2)线段DM与AM有怎样的位置关系?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com