
分析 先化为顶点式,再利用二次函数的性质判定,直接填空即可.
解答 解:抛物线y=2x2-3x-5=2(x-$\frac{3}{4}$)2-$\frac{31}{8}$,开口向向上,对称轴是x=$\frac{3}{4}$,顶点坐标为($\frac{3}{4}$,-$\frac{31}{8}$),当>$\frac{3}{4}$时,y随x增大而增大,当x<$\frac{3}{4}$时,y随x增大而减小.
故答案为:向上,直线x=$\frac{3}{4}$,($\frac{3}{4}$,-$\frac{31}{8}$),>$\frac{3}{4}$,<$\frac{3}{4}$.
点评 本题主要考查了二次函数的性质,解题的关键是熟记二次函数的性质.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
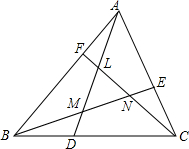 如图,D、E、F分别在△ABC的BC、CA、AB边上,$\frac{BD}{DC}$=$\frac{AF}{FB}$=$\frac{CE}{AE}$=λ,AD、BE、CF交成的三角形为LMN,求S△LMN(用S△ABC表示)
如图,D、E、F分别在△ABC的BC、CA、AB边上,$\frac{BD}{DC}$=$\frac{AF}{FB}$=$\frac{CE}{AE}$=λ,AD、BE、CF交成的三角形为LMN,求S△LMN(用S△ABC表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com