
 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )| A. | 12.5° | B. | 15° | C. | 20° | D. | 22.5° |
分析 根据平行四边形的性质和圆的半径相等得到△AOB为等边三角形,根据等腰三角形的三线合一得到∠BOF=∠AOF=30°,根据圆周角定理计算即可.
解答 解: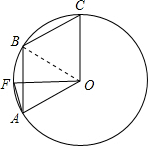 连接OB,
连接OB,
∵四边形ABCO是平行四边形,
∴OC=AB,又OA=OB=OC,
∴OA=OB=AB,
∴△AOB为等边三角形,
∵OF⊥OC,OC∥AB,
∴OF⊥AB,
∴∠BOF=∠AOF=30°,
由圆周角定理得∠BAF=$\frac{1}{2}$∠BOF=15°,
故选:B.
点评 本题考查的是圆周角定理、平行四边形的性质定理、等边三角形的性质的综合运用,掌握同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半、等腰三角形的三线合一是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 中位数是27 | B. | 众数是23和26 | C. | 极差是6 | D. | 平均数是24.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
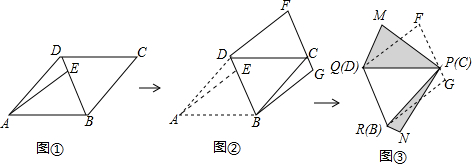
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
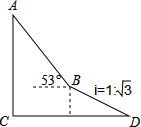 如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值).
如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
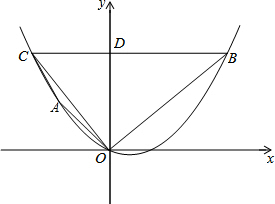 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx经过两点A(-1,1),B(2,2).过点B作BC∥x轴,交抛物线于点C,交y轴于点D.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx经过两点A(-1,1),B(2,2).过点B作BC∥x轴,交抛物线于点C,交y轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-1,0) | C. | (-1,-1) | D. | (-2,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com