
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() 在抛物线
在抛物线![]() (
(![]() )上,且
)上,且![]() ,
,
(1)若![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)若该抛物线与![]() 轴交于点
轴交于点![]() ,其对称轴与
,其对称轴与![]() 轴交于点
轴交于点![]() ,试求出
,试求出![]() ,
,![]() 的数量关系;
的数量关系;
(3)将该抛物线平移,平移后的抛物线仍经过![]() ,点
,点![]() 的对应点
的对应点![]() ,当
,当![]() 时,求平移后抛物线的顶点所能达到的最高点的坐标.
时,求平移后抛物线的顶点所能达到的最高点的坐标.
【答案】(1)b=1,c=3;(2)![]() ;(3)(
;(3)(![]() ,
,![]() )
)
【解析】
(1)把![]() 代入
代入![]() 得
得![]() ,与
,与![]() 构成方程组,解方程组即可求得;
构成方程组,解方程组即可求得;
(2)求得![]() ,
,![]() ,
,![]() ,即可得到
,即可得到![]() ,
,![]() ,即可求得
,即可求得![]() ;
;
(3)把![]() 化成顶点式,得到
化成顶点式,得到![]() ,根据平移的规律得到
,根据平移的规律得到![]() ,把
,把![]() 代入,进一步得到
代入,进一步得到![]() ,即
,即![]() ,分类求得
,分类求得![]() ,由
,由![]() ,得到
,得到![]() ,即
,即![]() ,从而得到平移后的解析式为
,从而得到平移后的解析式为![]() ,得到顶点为
,得到顶点为![]() ,
,![]() ,设
,设![]() ,即
,即![]() ,即可得到
,即可得到![]() 取最大值为
取最大值为![]() ,从而得到最高点的坐标.
,从而得到最高点的坐标.
解:(1)把![]() 代入
代入![]() ,可得
,可得![]() ,
,
解![]() ,可得
,可得![]() ,
,![]() ;
;
(2)由![]() ,得
,得![]() .
.
对于![]() ,
,
当![]() 时,
时,![]() .
.
抛物线的对称轴为直线![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
因为![]() ,
,
所以![]() ,
,![]() ,
,
![]() ;
;
(3)由平移前的抛物线![]() ,可得
,可得
![]() ,即
,即![]() .
.
因为平移后![]() 的对应点为
的对应点为![]()
可知,抛物线向左平移![]() 个单位长度,向上平移
个单位长度,向上平移![]() 个单位长度.
个单位长度.
则平移后的抛物线解析式为![]() ,
,
即![]() .
.
把![]() 代入,得
代入,得![]() .
.
![]() .
.
![]() ,
,
所以![]() .
.
当![]() 时,
时,![]() (不合题意,舍去);
(不合题意,舍去);
当![]() 时,
时,![]() ,
,
因为![]() ,所以
,所以![]() .
.
所以![]() ,
,
所以平移后的抛物线解析式为![]() .
.
即顶点为![]() ,
,![]() ,
,
设![]() ,即
,即![]() .
.
因为![]() ,所以当
,所以当![]() 时,
时,![]() 随
随![]() 的增大而增大.
的增大而增大.
因为![]() ,
,
所以当![]() 时,
时,![]() 取最大值为
取最大值为![]() ,
,
此时,平移后抛物线的顶点所能达到的最高点坐标为![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】在国家政策的调控下,某市的商品房成交均价由今年5月份的每平方米10000元下降到7月份的每平方米8100元.
(1)求6、7两月平均每月降价的百分率;
(2)如果房价继续回落,按此降价的百分率,请你预测到9月份该市的商品房成交均价是否会跌破每平方米6500元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
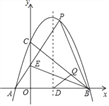
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,4).
(1)求此抛物线的解析式;
(2)设点P(2,n)在此抛物线上,AP交y轴于点E,连接BE,BP,请判断△BEP的形状,并说明理由;
(3)设抛物线的对称轴交x轴于点D,在线段BC上是否存在点Q,使得△DBQ成为等腰直角三角形?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】松雷中学校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,下图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元的人数共39人.
(1)他们一共抽查了多少人?
(2)若该校共有2310名学生,请估计全校学生共捐款多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.
(1)如图1,若∠ABC=90°,求证:OE∥AC;
(2)如图2,已知AB=AC,若sin∠ADE=![]() , 求tanA的值.
, 求tanA的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
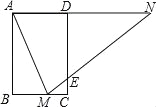
【题目】如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E
(1)求证:△AMN是等腰三角形;
(2)求BMAN的最大值;
(3)当M为BC中点时,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
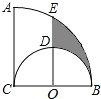
【题目】如图,![]() ,
,![]() ,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作
,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作![]() ,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是
,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com