
【题目】赵化鑫城某超市购进了一批单价为16元的日用品,销售一段时间后,为获得更多的利润,商场决定提高销售的价格,经试验发现,若按每件20元销售,每月能卖360件;若按每件25元销售,每月能卖210件;若每月的销售件数y(件)与价格x(元/件)满足y=kx+b.
(1)求出k与b的值,并指出x的取值范围?
(2)为了使每月获得价格利润1920元,商品价格应定为多少元?
(3)要使每月利润最大,商品价格又应定为多少?最大利润是多少?
【答案】(1)k=﹣30,b=960,x取值范围为16≤x≤32;(2)商品的定价为24元;(3)商品价格应定为24元,最大利润是1920元.
【解析】
(1)根据待定系数法求解即可;根据单价不低于进价(16元)和销售件数y≥0可得关于x的不等式组,解不等式组即得x的取值范围;
(2)根据每件的利润×销售量=1920,可得关于x的方程,解方程即可求出结果;
(3)设每月利润为W元,根据W=每件的利润×销售量可得W与x的函数关系式,然后根据二次函数的性质解答即可.
解:(1)由题意,得:![]() ,解得:
,解得:![]() ,∴y=﹣30x+960,
,∴y=﹣30x+960,
∵y≥0,∴﹣30x+960≥0,解得:x≤32,
又∵x≥16,∴x的取值范围是:16≤x≤32;
答:k=﹣30,b=960,x取值范围为:16≤x≤32;
(2)由题意,得:(﹣30x+960)(x﹣16)=1920,解得:x1=x2=24,
答:商品的定价为24元;
(3)设每月利润为W元,由题意,得:W=(﹣30x+960)(x﹣16)=﹣30(x﹣24)2+1920.
∵﹣30<0,∴当x=24时,W最大=1920.
答:商品价格应定为24元,最大利润是1920元.


科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西物产丰富,在历史传承与现代科技进步中,特色农林牧业、农产品加工业、传统手工业不断发展革新,富有地域特色和品牌的士特产品愈加丰富.根据市场调查,下面五种特产比较受人们的青睐:![]() 山西汾酒、
山西汾酒、![]() 山西老陈醋、
山西老陈醋、![]() 晋中平遥牛肉、
晋中平遥牛肉、![]() 山西沁州黄小米、
山西沁州黄小米、![]() 运城芮城麻片,某学校老师带领学生在集市上随机调查了部分市民对“我最喜爱的特产”进行投票,将票数进行统计.绘制了如图所示的条形统计图和扇形统计图(均不完整).
运城芮城麻片,某学校老师带领学生在集市上随机调查了部分市民对“我最喜爱的特产”进行投票,将票数进行统计.绘制了如图所示的条形统计图和扇形统计图(均不完整).


请根据图中的信息解答下列问题.
![]() 直接写出参与投票的人数,并补全条形统计图;
直接写出参与投票的人数,并补全条形统计图;
![]() 若该集市上共有
若该集市上共有![]() 人,请估计该集市喜爱运城芮城麻片的人数;
人,请估计该集市喜爱运城芮城麻片的人数;
![]() 若要从这五种特产中随机抽取出两种特产,请用画树状图或列表的方法,求正好抽到山西汾酒和晋中平遥牛肉的概率.
若要从这五种特产中随机抽取出两种特产,请用画树状图或列表的方法,求正好抽到山西汾酒和晋中平遥牛肉的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应垃圾分类处理,改善生态环境,某小区将生活垃圾分成三类:厨余垃圾、可回收垃圾和其他垃圾,分别记为a,b,c,并且设置了相应的垃圾箱,“厨余垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C
(1)小明将垃圾分装在三个袋中,任意投放,用画树状图或列表的方法求把三个袋子都放错位置的概率是多少?
(2)某学习小组为了了解居民生活垃圾分类投放的情况,现随机抽取了某天三类垃圾箱中总共100吨的生活垃圾,数据统计如表(单位:吨):
A | B | C | |
a | 40 | 10 | 10 |
b | 3 | 24 | 3 |
c | 2 | 2 | 6 |
调查发现,在“可回收垃圾”中塑料类垃圾占10%,每回收1吨塑料类垃圾可获得0.7吨二级原料,某城市每天大约产生200吨生活垃圾假设该城市每天处理投放正确的垃圾,每天大概可回收多少吨塑料类垃圾的二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
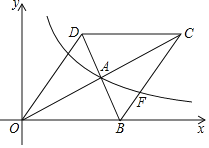
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=![]() (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(3,4),则点F的坐标是_____.
(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(3,4),则点F的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E是CD边上一点,![]() ,连接AE、BE、BD,且AE、BD交于点F.若
,连接AE、BE、BD,且AE、BD交于点F.若![]() ,则
,则![]() ( )
( )
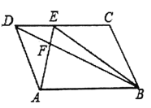
A.15.5B.16.5C.17.5D.18.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
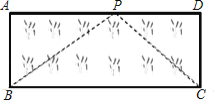
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
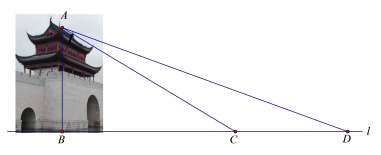
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O为BC边上一点,⊙O经过A、B两点,与BC边交于点E,点F为BE下方半圆弧上一点,FE⊥AC,垂足为D,∠BEF=2∠F.

(1)求证:AC为⊙O切线.
(2)若AB=5,DF=4,求⊙O半径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com