
分析 利用待定系数法求一次函数解析式得出即可;
(1)利用一次函数增减性得出即可.
(2)根据题意得出n=-2m+2,联立方程,解方程即可求得.
解答 解:设解析式为:y=kx+b,
将(1,0),(0,2)代入得:$\left\{\begin{array}{l}{k+b=0}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$,
∴这个函数的解析式为:y=-2x+2;
(1)把x=-2代入y=-2x+2得,y=6,
把x=3代入y=-2x+2得,y=-4,
∴y的取值范围是-4≤y<6.
(2)∵点P(m,n)在该函数的图象上,
∴n=-2m+2,
∵m-n=4,
∴m-(-2m+2)=4,
解得m=2,n=-2,
∴点P的坐标为(2,-2).
点评 本题考查了待定系数法求一次函数的解析式,一次函数图象上点的坐标特征以及一次函数的性质,求得解析式上解题的关键.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案科目:初中数学 来源: 题型:填空题
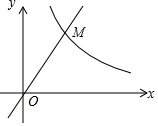 如图,点M是函数y=$\sqrt{3}$x与y=$\frac{k}{x}$的图象在第一象限内的交点,OM=4,则k的值为4$\sqrt{3}$.
如图,点M是函数y=$\sqrt{3}$x与y=$\frac{k}{x}$的图象在第一象限内的交点,OM=4,则k的值为4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:$\frac{x+1}{{{x^2}-1}}$÷$\frac{2}{x-1}$;
(1)计算:$\frac{x+1}{{{x^2}-1}}$÷$\frac{2}{x-1}$;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若x=y,则x+c=y-c | B. | 若x=y,则xc=yc | ||
| C. | 若x=y,则$\frac{x}{c}=\frac{y}{c}$ | D. | 若$\frac{x}{2c}=\frac{y}{3c}$,则2x=3y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 比赛场次 | 胜场 | 负场 | 积分 |
| m | 0 | m | m |
| 8 | 3 | 5 | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
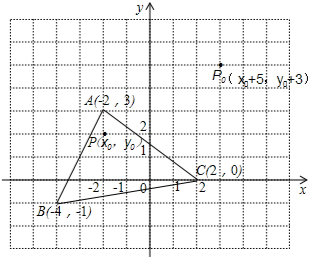 如图,三角形ABC中任意一点P(x0,y0)经平移后对应点P1(x0+5,y0+3).将三角形ABC作同样的平移得到三角形A1B1C1.
如图,三角形ABC中任意一点P(x0,y0)经平移后对应点P1(x0+5,y0+3).将三角形ABC作同样的平移得到三角形A1B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
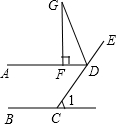 如图,直线AD∥BC,点C、D、E在同一条直线上,∠ADE的角平分线DG与直线AD的垂线(垂足为点F)相交于点G,若∠G=25°,则∠1的度数是( )
如图,直线AD∥BC,点C、D、E在同一条直线上,∠ADE的角平分线DG与直线AD的垂线(垂足为点F)相交于点G,若∠G=25°,则∠1的度数是( )| A. | 50° | B. | 30° | C. | 25° | D. | 15° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com