
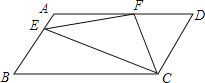
【题目】如图所示,在平行四边形ABCD中,![]() ,F是AD的中点,作
,F是AD的中点,作![]() ,垂足E在线段上,连接EF、CF,则下列结论
,垂足E在线段上,连接EF、CF,则下列结论![]() ;
;![]() ;
;![]() ,
,![]() 中一定成立的是______
中一定成立的是______ ![]() 把所有正确结论的序号都填在横线上
把所有正确结论的序号都填在横线上![]()
【答案】![]()
【解析】
由在平行四边形ABCD中,AD=2AB,F是AD的中点,易得AF=FD=CD,继而证得①∠DCF=![]() ∠BCD;然后延长EF,交CD延长线于M,分别利用平行四边形的性质以及全等三角形的判定与性质得出△AEF≌△DMF(ASA),得出对应线段之间关系,进而得出答案.
∠BCD;然后延长EF,交CD延长线于M,分别利用平行四边形的性质以及全等三角形的判定与性质得出△AEF≌△DMF(ASA),得出对应线段之间关系,进而得出答案.
①∵F是AD的中点,
∴AF=FD,
∵在ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF=![]() ∠BCD,
∠BCD,
即∠BCD=2∠DCF;故此选项错误;
②延长EF,交CD延长线于M,
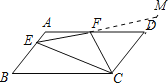
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
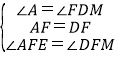 ,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=FM,故②正确;
③设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°-x,
∴∠EFC=180°-2x,
∴∠EFD=90°-x+180°-2x=270°-3x,
∵∠AEF=90°-x,
∴∠DFE=3∠AEF,故此选项正确.
④∵EF=FM,
∴S△EFC=S△CFM,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误;
综上可知:一定成立的是②③,
故答案为:②③.


科目:初中数学 来源: 题型:
【题目】阅读以下材料:
高斯是德国著名的大科学家,他最出名的故事就是在他10岁时,小学老师出了一道算术难题:计算1+2+3+……+100=?
在其他同学还在犯难时,却很快传来了高斯的声音:“老师,我已经算好了!”
老师很吃惊,高斯解释道:因为1+100=101,2+99=101,3+98=101,……,49+52=101,50+51=101,而像这样的等于101的组合一共有50组,所以答案很快就可以求出:101×50=5050。
根据以上的信息,请同学们:
(1)计算1+3+5+7+…+99的值.
(2)计算2+4+6+8+…+200的值.
(3)用含a和n的式子表示运算结果:求a+2a+3a+…+na的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一小题计分.
①若单项式﹣xmyn+4 与 5x2y 是同类项,则 nm 的值为____.
②实施西部大开发战略是党中央的重大决策,我国国土面积约为960 万平方千米,而我国西部地区的面积占我国国土面积的 ![]() ,用科学记数法表示我国西部地区的面积约为_____平方千米.
,用科学记数法表示我国西部地区的面积约为_____平方千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣ ![]() x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).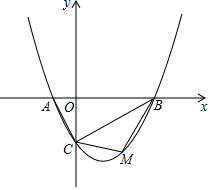
(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标;
(3)试探究:△ABC的外接圆的圆心位置,并求出圆心坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将背面相同,正面分别标有数字1,2,3,4的四张卡片洗匀后,背面朝上放在桌面上.
(1)从中随机抽取一张卡片,求该卡片正面上的数字是偶数的概率;
(2)先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①两边和其中一边的对角对应相等的两个三角形全等.
②角的对称轴是角平分线
③两边对应相等的两直角三角形全等
④成轴对称的两图形一定全等
⑤到线段两端距离相等的点在线段的垂直平分线上,
正确的有![]()
![]() 个.
个.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
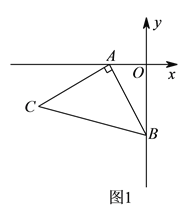
【题目】如图![]() ,
, ![]() ,
, ![]() ,以
,以![]() 点为顶点、
点为顶点、![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() .
.
(![]() )求
)求![]() 点的坐标.
点的坐标.
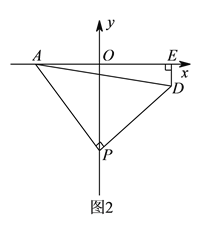
(![]() )如图
)如图![]() ,
, ![]() 为
为![]() 轴负半轴上一个动点,当
轴负半轴上一个动点,当![]() 点沿
点沿![]() 轴负半轴向下运动时,以
轴负半轴向下运动时,以![]() 为顶点,
为顶点, ![]() 为腰作等腰
为腰作等腰![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,求
点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=4 ![]() ,BC=6,∠B=45°,D为BC边上一动点,将△ABC沿着过点D的直线折叠使点C落在AB边上,则CD的取值范围是 .
,BC=6,∠B=45°,D为BC边上一动点,将△ABC沿着过点D的直线折叠使点C落在AB边上,则CD的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com