
 已知:菱形的两条对角线的长分别为a,b,面积为S.
已知:菱形的两条对角线的长分别为a,b,面积为S.分析 根据菱形的两条对角线互相垂直平分得出AC⊥BD,OA=OC=$\frac{1}{2}$AC=$\frac{1}{2}$a,再由菱形的面积S=S△ABD+S△CBD,根据三角形的面积=底×高,代入即可证明.
解答  证明:如图.
证明:如图.
∵四边形ABCD是菱形,AC=a,BD=b,
∴AC⊥BD,OA=OC=$\frac{1}{2}$AC=$\frac{1}{2}$a,
∴菱形的面积S=S△ABD+S△CBD
=$\frac{1}{2}$BD•OA+$\frac{1}{2}$BD•OC
=$\frac{1}{2}$b•$\frac{1}{2}$a+$\frac{1}{2}$b•$\frac{1}{2}$a
=$\frac{1}{2}$ab.
点评 本题考查了菱形的性质,掌握菱形的两条对角线互相垂直平分是解题的关键,本题实际上证明了菱形的面积等于两对角线乘积的一半.


科目:初中数学 来源: 题型:解答题
 某市为加固长90米,高30米,坝顶宽为6米,迎水坡和背水坡都是1:1的横断面是梯形的防洪大坝,要将大坝加高2米,背水坡坡度改为1:1.5,已知坝顶宽不变,求大坝横戴面积增加多少平方米?
某市为加固长90米,高30米,坝顶宽为6米,迎水坡和背水坡都是1:1的横断面是梯形的防洪大坝,要将大坝加高2米,背水坡坡度改为1:1.5,已知坝顶宽不变,求大坝横戴面积增加多少平方米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
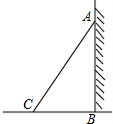 如图,一架长为10m的梯子AB斜靠在墙上,梯子的顶端距地面的垂直距离为8m.
如图,一架长为10m的梯子AB斜靠在墙上,梯子的顶端距地面的垂直距离为8m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com