
【题目】风筝又称“纸鸢”、“鸢儿”,放风筝是民间传统游戏之一,也是清明时节人们所喜爱的活动.小李打算抓住这一机遇,以每个20元的成本制作了30个风筝,再以每个40元的价格售出,很快就被一抢而空,于是小李计划加紧制作第二批风筝.
(1)预计第二批风筝的成本是每个15元,仍以原价出售,若两批风筝的总利润不低于2850元,则第二批至少应该制作多少个风筝?
(2)在实际制作过程中,小李按照(1)中风筝的最低数量进行制作,但制作风筝的成本比预期的15元多了a%(a>10),于是小李决定将售价也提高a%,附近的商户受到小李的启发,也纷纷卖起了风筝,在市场冲击下,小李实际还剩下![]() a%的风筝没卖出去,但仍然比第一次获利多1668元,求a的值.
a%的风筝没卖出去,但仍然比第一次获利多1668元,求a的值.
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
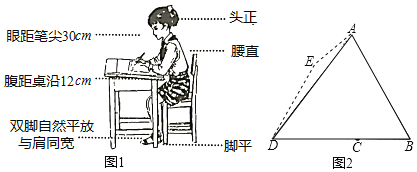
【题目】我们知道良好的坐姿有利于青少年骨骼生长,有利于身体健康,那么首先要有正确的写字坐姿,身子上半部坐直,头部端正、目视前方,两手放在桌面上,两腿平放,胸膛挺起,理想状态下,如图1所示,将图1中的眼睛记为点A,腹记为点B,笔尖记为点D,且BD与桌沿的交点记为点C
(1)若∠ADB=53°,∠B=60°,求A到BD的距离及C、D两点间的距离(结果精确到1cm).
(2)老师发现小红同学写字姿势不正确,眼睛倾斜至图2的点E,点E正好在CD的垂直平分线上,且∠BDE=60°,于是要求其纠正为正确的姿势.求眼睛所在的位置应上升的距离.(结果精确到1cm)
参考数据:sin53°≈0.80,cos53°≈0.60,.tan53°≈1.33,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张背面完全相同的卡片,正面上分别标有数字﹣2,﹣1,1,2.把这四张卡片背面朝上,随机抽取一张,记下数字为m;放回搅匀,再随机抽取一张卡片,记下数字为n,则y=mx+n不经过第三象限的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 中的
中的![]() ,
,![]() 满足下表
满足下表
| … |
| 0 | 1 | 2 | 3 | … |
| … | 0 |
|
|
|
| … |
(l)![]() ________,
________,![]() ________;
________;
(2)函数图象对称轴是____________;
(3)如果点![]() ,
,![]() 是图象上点,则
是图象上点,则![]() ________;
________;
(4)函数图象与![]() 轴交于点
轴交于点![]() 、点
、点![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,则点
,则点![]() 坐标为________.
坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某路段上有A,B两处相距近200m且未设红绿灯的斑马线.为使交通高峰期该路段车辆与行人的通行更有序,交通部门打算在汽车平均停留时间较长的一处斑马线上放置移动红绿灯.图1,图2分别是交通高峰期来往车辆在A,B斑马线前停留时间的抽样统计图.根据统计图解决下列问题:
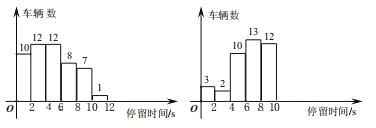
(1)若某日交通高峰期共有350辆车经过A斑马线,请估计该日停留时间为10s~12s的车辆数,以及这些停留时间为10s~12s的车辆的平均停留时间;(直接写出答案)
(2)移动红绿灯放置在哪一处斑马线上较为合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
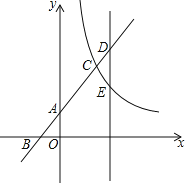
【题目】如图所示,直线y=x+2与坐标轴交于A、B两点,与反比例函数y=![]() (x>0)交于点C,已知AC=2AB.
(x>0)交于点C,已知AC=2AB.
(1)求反比例函数解析式;
(2)若在点C的右侧有一平行于y轴的直线,分别交一次函数图象与反比例函数图象于D、E两点,若CD=CE,求点D坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是
是![]() 的角平分线,点
的角平分线,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,
,![]()
(1)如图1,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,若![]() 为等边三角形,在不添加辅助线的情况下,请你直接写出所有的全等三角形.
为等边三角形,在不添加辅助线的情况下,请你直接写出所有的全等三角形.
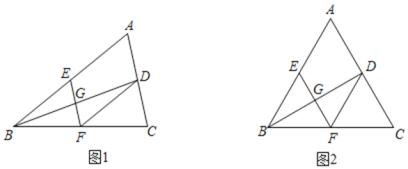
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com