
分析 (1)根据题意可以设出未知数,列出相应的方程组,从而可以解答本题;
(2)根据题意可以列出相应的不等式,从而可以解答本题.
解答 解:(1)设每个甲种零件的价格是x元,每个乙种零件的价格是y元,
$\left\{\begin{array}{l}{3x+y=44}\\{x+2y=38}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=10}\\{y=14}\end{array}\right.$,
答:每个甲种零件的价格是10元,每个乙种零件的价格是14元;
(2)设购买甲种零件a个,
10a+14(20-a)≤230,
解得,a≥12.5,
∴甲种零件最少购买13个,
答:甲种零件最少购买13个.
点评 本题考查一元一次不等式的应用、二元一次方程组的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用不等式的性质和方程的思想解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
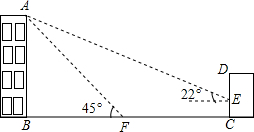 如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)
如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
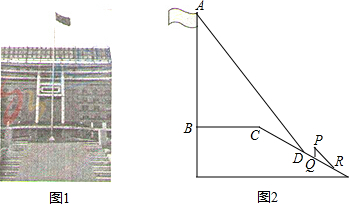
 我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)
我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com