
科目:初中数学 来源: 题型:解答题
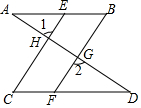 如图,已知AB∥CD,∠B=∠C,求证:∠1=∠2.
如图,已知AB∥CD,∠B=∠C,求证:∠1=∠2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
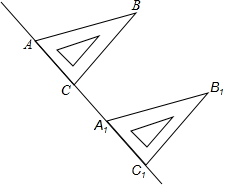 如图,同学们用直尺和三角板画平行线,将一块三角板ABC的一边AC贴着直尺推移到A1B1C1的位置.
如图,同学们用直尺和三角板画平行线,将一块三角板ABC的一边AC贴着直尺推移到A1B1C1的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
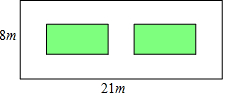 某小区有一块长21米,宽8米的矩形空地,如图所示.社区计划在其中修建两块完全相同的矩形绿地,并且两块绿地之间及四周都留有宽度为x米的人行通道.如果这两块绿地的面积之和为60平方米,人行通道的宽度应是多少米?
某小区有一块长21米,宽8米的矩形空地,如图所示.社区计划在其中修建两块完全相同的矩形绿地,并且两块绿地之间及四周都留有宽度为x米的人行通道.如果这两块绿地的面积之和为60平方米,人行通道的宽度应是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
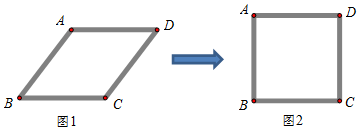 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,接着活动学具成为图2所示正方形,并测得对角线AC=40cm,则图1中对角线AC的长为 ( )
小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,接着活动学具成为图2所示正方形,并测得对角线AC=40cm,则图1中对角线AC的长为 ( )| A. | 20 cm | B. | 30 cm | C. | 40 cm | D. | $20\sqrt{2}$cm |
查看答案和解析>>
科目:初中数学 来源:2017届湖北省大冶市九年级3月月考数学试卷(解析版) 题型:判断题
如图1,在菱形ABCD中,AC=2,BD=2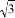 ,AC,BD相交于点O.
,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.
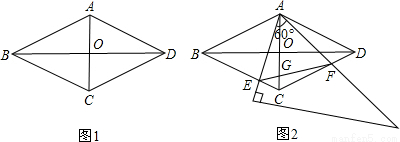
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省揭阳市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列多项式乘法算式中,可以用平方差公式计算的是 ( )
A. (m-n)(n-m) B. (a+b)(-a-b)
C. (-a-b)(a-b) D. (a+b)(a+b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com