
阅读以下的材料:
如果两个正数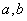 ,即
,即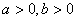 ,有下面的不等式:
,有下面的不等式:
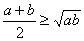 当且仅当
当且仅当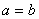 时取到等号
时取到等号
我们把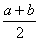 叫做正数
叫做正数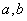 的算术平均数,把
的算术平均数,把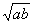 叫做正数
叫做正数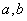 的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
例:已知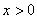 ,求函数
,求函数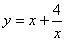 的最小值。
的最小值。
解:令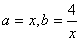 ,则有
,则有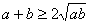 ,得
,得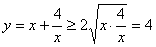 ,当且仅当
,当且仅当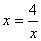 时,即
时,即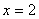 时,函数有最小值,最小值为
时,函数有最小值,最小值为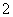 。
。
根据上面回答下列问题
① 已知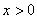 ,则当
,则当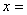 时,函数
时,函数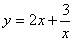 取到最小值,最小值
取到最小值,最小值
为 ;
② 用篱笆围一个面积为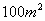 的矩形花园,问这个矩形的长、宽各为多
的矩形花园,问这个矩形的长、宽各为多 少时,所
少时,所
用的篱笆最短,最短的篱 笆周长是多少;
笆周长是多少;
③. 已知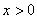 ,则自变量
,则自变量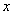 取何值时,函数
取何值时,函数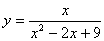 取到最大值,最大值为多少?
取到最大值,最大值为多少?
科目:初中数学 来源: 题型:
己知1纳米= 0.000000001米,则27纳米用科学记数法表示为( ).
0.000000001米,则27纳米用科学记数法表示为( ).
A. 27×10-9 B. 2.7×10-8 C. 2.7×10-9 D. -2.7×108
查看答案和解析>>
科目:初中数学 来源: 题型:
下面是按一定规律排列的一列数:
第1个数: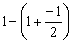 ; 第2个数:
; 第2个数:

 ;
;
第3个数:


 ;…… ;
;…… ;
(1)分别计算这三个数的结果(直接写答案)
(2)写出第2010个数的形式(中间部分用省略号,两端部分必须写详细),然后推测出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图5310,一枚直径为4 cm的圆形古钱币沿着直线滚动一周,圆心移动的距离是( )
A.2π cm B.4π cm C.8π cm D.16π cm
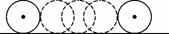
查看答案和解析>>
科目:初中数学 来源: 题型:
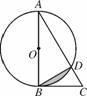
如图5316,在△ABC中,以AB为直径的⊙O交AC于点D,∠DBC=∠BAC.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为2,∠BAC=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
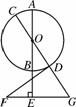
如图5219,AB,CD是⊙O的直径,点E在AB的延长线上,FE⊥AB,BE=EF=2,FE的延长线交CD的延长线于点G,DG=GE=3,连接FD.
(1)求⊙O的半径;
(2)求证:DF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校。在课堂上,李老师请学生画出自行车行进路程s千米与行进时间t的函数图像的示意图,同学们画出的示意图如下,你认为正确的是 ( )
 |  | ||||||
 | |||||||
 | |||||||
A B C D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com