练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．先化简，再求值：3（x+y）2-（2x-y）（2x+y），其中x=-1，y=2．

    分析 根据完全平方公式和平方差公式可以化简题目中的式子，然后将x、y的值代入化简后的式子即可解答本题．

    解答 解：3（x+y）2-（2x-y）（2x+y）
    =3x2+6xy+3y2-4x2+y2
    =-x2+6xy+4y2，
    当x=-1，y=2时，原式=-（-1）2+6×（-1）×2+4×22=3．

    点评 本题考查整式的混合运算-化简求值，解答本题的关键是明确整式的化简求值的方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．已知：正方形ABCD，E为平面内任意一点，连接DE，将线段DE绕点D顺时针旋转90°得到DG，连接EC，AG．
    （1）当点E在正方形ABCD内部时，
    ①根依题意，在图1中补全图形；
    ②判断AG与CE的数量关系与位置关系并写出证明思路．
    （2）当点B，D，G在一条直线时，若AD=4，DG=2$\sqrt{2}$，求CE的长．（可在备用图中画图）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图1，在正方形ABCD的外侧，作两个等边三角形ADE和DCF，连接AF、BE．

    （1）请判断AF与BE的关系并给予证明；
    （2）如图2，若将条件“两个等边三角形ADE和DCF变为两个等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）问中的结论是否仍然成立？请作出判断并给予证明；
    （3）若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论是否仍然成立？请直接写出判断结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

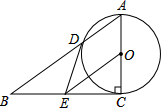    4．如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，点E为BC的中点，连接DE．
    （1）求证：DE是⊙O的切线；
    （2）若EC=3，BD=2$\sqrt{6}$，求AC的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，在△ABC中，OA=OC=3，∠BOC=90°，且点A，C分别在x轴，y轴的正半轴上，抛物线y=-x2+bx+c恰好经过点A和点C，与x轴交于另一点B．
    （1）求抛物线的解析式；
    （2）点E为第一象限内抛物线上一点，设△ABC的面积为S1，△BCE的面积为S2，若S1=2S2，求点E的坐标；
    （3）设抛物线的顶点为M，在抛物线的对称轴上是否存在点P，使点M关于直线AP的对称点恰好落在x轴上？若存在，请直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

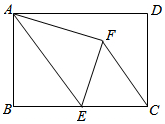    1．如图，在矩形ABCD中，AB=5，BC=8，点E为BC上一动点，把△ABE沿AE折叠；若点E是BC边的中点，点B落在点F处，连接CF．
    （1）求证：AE∥CF．
    （2）求Sin∠ECF的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知关于x的一元二次方程2x2-4mx+2m2+3m-2=0有两个实数根．
    （1）求实数m的取值范围；
    （2）设x1，x2是原方程的两个实数根，当m为何值时，x12+x22有最小值？并求这个最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．抛掷一枚均匀的正方体骰子一次，下列3个事件：①向上一面的点数不小于3；②向上一面的点数是偶数；③向上一面的点数是3的倍数，其中发生的可能性最大的事件是①．（填写你认为正确的序号即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．写出日常生活现象中的数学原理：
    有人和你打招呼，你笔直向他走过去两点之间线段最短
    要用两个钉子把毛巾架安装在墙上两点确定一条直线
    桥建造的方向通常是垂直于河两岸夹在两平行线间的线段中，垂线段最短
    人去河边打水总是垂直于河边方向走直线外一点和直线上各点的连线中，垂线段最短

    查看答案和解析>>

    同步练习册答案