
分析 (1)直接利用求根公式计算即可;
(2)参照(1)中的解法解题即可.
解答 解:(1)2x2-7x+6=0,
∵△=49-48=1>0,
∴x=$\frac{7±1}{4}$,
∴x1=2,x2=$\frac{3}{2}$,
∴满足要求的矩形B存在.
故答案为2,$\frac{3}{2}$;
(2)设所求矩形的两边分别是x和y,由题意,得
$\left\{\begin{array}{l}{x+y=\frac{3}{2}}\\{xy=1}\end{array}\right.$,
消去y化简,得
2x2-3x+2=0,
∵△=9-16<0,
∴不存在矩形B.
点评 本题考查了根的判别式,此类题目要读懂题意,准确的找到等量关系列方程组,要会灵活运用根的判别式在不解方程的情况下判断一元二次方程的解的情况.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
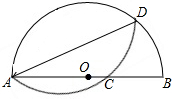 如图,半圆的直径AB=10cm,把弓形沿AD对折,交直径AB于C.若AC=6,则AD的长( )
如图,半圆的直径AB=10cm,把弓形沿AD对折,交直径AB于C.若AC=6,则AD的长( )| A. | 4$\sqrt{5}$ | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com