
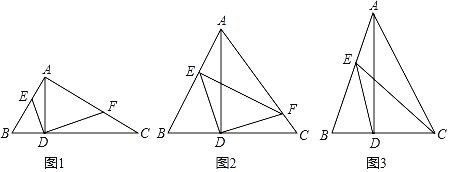
【题目】△ABC中,AD⊥BC,E,F分别在AB,AC上.
(1)已知:DE⊥DF
①如图1:若AB⊥AC,求证:△DAE~△DFC.
②连EF,若FE⊥AB于E(如图2),且BD:CD:DA=2:3:4,EF=4![]() ,求BC的长.
,求BC的长.
(2)连EC,DE平分∠BEC(如图3),且AD=2CD,CE=2AE,若DE=10,求AC的长.
【答案】(1)①详见解析;②![]() ;(2)2
;(2)2![]() .
.
【解析】
(1)①由互余的性质可求∠ADE=∠CDF,∠DAE=∠C,即可证△DAE~△DFC;
②由BD:CD:DA=2:3:4,可设BD=2k,CD=3k,DA=4k,作CG⊥AB,得:FE∥CG,由对应线段成比例可得:AE:AF=1:![]() ,求出AE,AF,再由△CFN∽△CAD,△DME∽△DNF即可求解;
,求出AE,AF,再由△CFN∽△CAD,△DME∽△DNF即可求解;
(2)由于CE=2AE,可取EC中点K,连接AK交BC于H,过点E作EM⊥AH于M,过点D作DN⊥AH于N,应用等腰三角形性质和角平分线易证AH∥DE,△CKH∽△CED,△DHN∽△AHD,再结合勾股定理可求得AC.
证明:(1)①如图1,
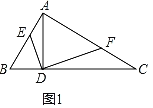
∵DE⊥DF,AD⊥BC,AB⊥AC,
∴∠BAD+∠DAC=90°,∠DAC+∠C=90°,∠ADF+∠ADE=90°,∠ADF+∠CDF=90°
∴∠ADE=∠CDF,∠DAE=∠C
∴△DAE~△DFC
②如图2,过点C作CG⊥AB于G,过点E作EM⊥AD于M,过点F作FN⊥BC于N,

∵BD:CD:DA=2:3:4,可设BD=2k,CD=3k,DA=4k,
由勾股定理得:AB![]() 2
2![]() k,AC
k,AC![]() 5k
5k
∵BC=AC=5k,CG⊥AB
∴AG=BG![]() AB
AB![]() k
k
∵FE⊥AB
∴FE∥CG
∴![]()
设AE![]() m,AF=5m,由勾股定理得:AE2+EF2=AF2,即:
m,AF=5m,由勾股定理得:AE2+EF2=AF2,即:![]() (5m)2,
(5m)2,
解得:m1=﹣2(舍去),m2=2;
∴AE=2![]() ,AF=10,
,AF=10,
∵EM⊥AD,AD⊥BC,
∴△AEM∽△ABD,
![]() ,即:
,即:![]()
∴EM=2,AM=4
∵AD⊥BC,FN⊥BC
∴△CFN∽△CAD
∴![]() ,即:
,即:![]()
∴FN=4k﹣8,CN=3k﹣6
∴DN=CD﹣CN=6
∵DE⊥DF,AD⊥BC
∴∠EDM+∠FDM=∠FDN+∠FDM=90°
∴∠EDM=∠FDN
∵∠DME=∠DNF=90°
∴△DME∽△DNF
∴![]() ,即:
,即:![]() ,解得:
,解得:![]() ,
,![]() (舍去);
(舍去);
∴BD=2![]() 5,CD=3
5,CD=3![]() ,BC=5
,BC=5![]()
(2)取EC中点K,连接AK交BC于H,过点E作EM⊥AH于M,过点D作DN⊥AH于N,如图3:
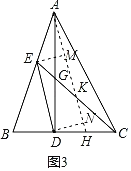
∵CE=2AE=2EK
∴AE=EK
∴∠BAH=∠AKE
∵∠BEC=∠BAH+∠AKE
∴∠BEC=2∠BAH
∵DE平分∠BEC
∴∠BEC=2∠BED
∴∠BED=∠BAH
∴AH∥ED
∴△CKH∽△CED,∠GAK=∠GDE
∴![]() ,即:
,即:![]()
∴KH=5,CH![]() CD
CD
∵EM⊥AH,DN⊥AH
∴EM∥DN,∠EMN=∠DNM=90°
∵AH∥ED
∴∠EDN=90°
∴DEMN是矩形,
∴MN=DE=10
∵AK=EK,EM⊥AK
∴AM=MK
∵AD=2CD,设CD=2m,则DH=m,AD=4m,AH![]() m,DN
m,DN![]() m,
m,
∵AD⊥BC,DH⊥AH
∴△DHN∽△AHD
∴![]() ,即:HN
,即:HN![]() m,KN=5
m,KN=5![]() m,AM=MK=5
m,AM=MK=5![]() m,AH=AM+MN+HN=5
m,AH=AM+MN+HN=5![]() m+10
m+10![]() m=15
m=15![]() m
m
∵AD2+DH2=AH2
∴(4m)2+m2![]() ,解得:
,解得:![]() (舍去),
(舍去),![]()
∴CD=2![]() ,AD=4
,AD=4![]() ,
,
∴AC![]() 2
2![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F分别是边AD、AB上的点,连结OE、OF、EF.若AB=7,BC=5![]() ,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.
,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴分别交于A(﹣3,0),B两点,与y轴交于点C,抛物线的顶点E(﹣1,4),对称轴交x轴于点F.
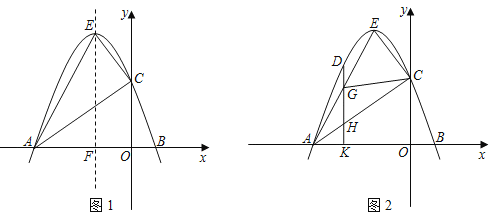
(1)请直接写出这条抛物线和直线AE、直线AC的解析式;
(2)连接AC、AE、CE,判断△ACE的形状,并说明理由;
(3)如图2,点D是抛物线上一动点,它的横坐标为m,且﹣3<m<﹣1,过点D作DK⊥x轴于点K,DK分别交线段AE、AC于点G、H.在点D的运动过程中,
①DG、GH、HK这三条线段能否相等?若相等,请求出点D的坐标;若不相等,请说明理由;
②在①的条件下,判断CG与AE的数量关系,并直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送花,感恩母亲,祝福母亲.今年节日前夕,某花店采购了一批康乃馨,经分析上一年的销售情况,发现这种康乃馨每天的销售量y(支)是销售单价x(元)的一次函数,已知销售单价为7元/支时,销售量为16支;销售单价为8元/支时,销售量为14支.
(1)求这种康乃馨每天的销售量y(支)关于销售单价x(元/支)的一次函数解析式;
(2)若按去年方式销售,已知今年这种康乃馨的进价是每支5元,商家若想每天获得42元的利润,销售单价要定为多少元?
(3)在(2)的条件下,当销售单价x为何值时,花店销售这种康乃馨每天获得的利润最大?并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节期间,某校倡议学生利用双休日“植树”劳动,为了解同学们劳动情况.学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回顾下列:
(1)通过计算,将条形图补充完整;
(2)扇形图形中“1.5小时”部分圆心角是 ;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家以A、B两种原料,利用不同的工艺手法生产出了甲、乙两种袋装产品,其中,甲产品每袋含1.5千克A原料、1.5千克B原料;乙产品每袋含2千克A原料、1千克B原料.甲、乙两种产品每袋的成本价分别为袋中两种原料的成本价之和.若甲产品每袋售价72元,则利润率为20%.某节庆日,厂家准备生产若干袋甲产品和乙产品,甲产品和乙产品的数量和不超过100袋,会计在核算成本的时候把A原料和B原料的单价看反了,后面发现如果不看反,那么实际成本比核算时的成本少500元,那么厂家在生产甲乙两种产品时实际成本最多为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:①若![]() 则
则![]() ②若
②若![]() 则
则![]() ③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )
③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com