
如图,△ABC中,AD⊥BC于D,且有下列条件:(1)∠B+∠DAC=90°;(2)∠B=∠DAC;(3)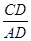 =
= ;(4)AB2=BD·BC其中一定能够判定△ABC是直角三角形的共有( )
;(4)AB2=BD·BC其中一定能够判定△ABC是直角三角形的共有( )
| A.3个 | B.2个 | C.1个 | D.0个 |
D.
解析试题分析:根据已知对各个条件进行分析,从而得到答案.
(1)不能,∵AD⊥BC,∴∠B+∠BAD=90°,∵∠B+∠DAC=90°,∴∠BAD=∠DAC,∴无法证明△ABC是直角三角形;
(2)能,∵∠B=∠DAC,则∠BAD=∠C,∴∠B+∠BAD=∠C+∠DAC=180°÷2=90°;
(3)能
∵CD:AD=AC:AB,∠ADB=∠ADC=90°,
∴Rt△ABD∽Rt△CAD(直角三角形相似的判定定理),
∴∠ABD=∠CAD;∠BAD=∠ACD
∵∠ABD+∠BAD=90°
∴∠CAD+∠BAD=90°
∵∠BAC=∠CAD+∠BAD
∴∠BAC=90°;
(4)能,
∵能说明△CBA∽△ABD,
∴△ABC一定是直角三角形.
共有3个.
故选D.
考点: 相似三角形的判定与性质


科目:初中数学 来源: 题型:单选题
在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm.如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为( )
| A.900cm | B.1000cm | C.1100cm | D.1200cm |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为
| A.1.5米 | B.2.3米 | C.3.2米 | D.7.8米 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树高AB为( )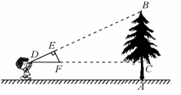
| A.12m | B.13.5m | C.15m | D.16.5m |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,在平行四边形ABCD中,AB=6,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且AB=3CF,DG⊥AE,垂足为G,若DG=2,则AE的边长为( )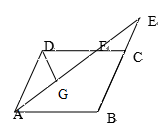
A.4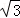 | B.6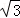 | C.6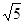 | D.4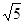 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,△ABC的三个顶点都在⊙O上,∠BAC的平分线交BC于点D,交⊙O于点E,则与△ABD相似的三角形有( )
| A.3个 | B.2个 | C.1个 | D.0个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com