
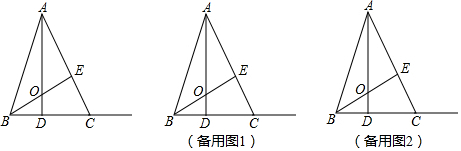
分析 (1)只要证明△AOE≌△BCE即可解决问题;
(2)分两种情形讨论求解即可①当点Q在线段BD上时,QD=2-4t,②当点Q在射线DC上时,DQ=4t-2时;
(3)分两种情形求解即可①如图2中,当OP=CQ时,BOP≌△FCQ.②如图3中,当OP=CQ时,△BOP≌△FCQ;
解答 解:(1)如图1中,
∵AD是高,
∴∠ADC=90°,
∵BE是高,
∴∠AEB=∠BEC=90°,
∴∠EAO+∠ACD=90°,∠EBC+∠ECB=90°,
∴∠EAO=∠EBC,
在△AOE和△BCE中,
$\left\{\begin{array}{l}{∠EAO=∠EBC}\\{AE=BE}\\{∠AEO=∠BEC}\end{array}\right.$,
∴△AOE≌△BCE,
∴AO=BC=5.
(2)∵BD=$\frac{2}{3}$CD,BC=5,
∴BD=2,CD=3,
由题意OP=t,BQ=4t,
①当点Q在线段BD上时,QD=2-4t,
∴S=$\frac{1}{2}$•t(2-4t)=-2t2+t(0<t<$\frac{1}{2}$).
②当点Q在射线DC上时,DQ=4t-2,
∴S=$\frac{1}{2}$•t(4t-2)=2t2-t($\frac{1}{2}$<t≤5).
(3)存在.
①如图2中,当OP=CQ时,∵OB=CF,∠POB=∠FCQ,∴△BOP≌△FCQ.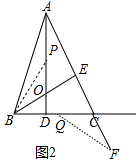
∴CQ=OP,
∴5-4t═t,
解得t=1,
②如图3中,当OP=CQ时,∵OB=CF,∠POB=∠FCQ,∴△BOP≌△FCQ.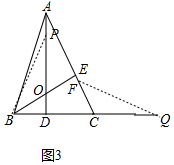
∴CQ=OP,
∴4t-5=t,
解得t=$\frac{5}{3}$.
综上所述,t=1或$\frac{5}{3}$s时,△BOP与△FCQ全等.
点评 本题考查三角形综合题、全等三角形的判定和性质、三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
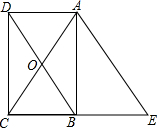 如图,矩形ABCD的对角线AC、BD相交于点O.过点A作AE∥BD,交CB的延长线于点E.
如图,矩形ABCD的对角线AC、BD相交于点O.过点A作AE∥BD,交CB的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 检测小食品质量应采用全面调查 | |
| B. | 从2万名考生中抽取100名考生作为样本,样本容量是2万 | |
| C. | 反映你本学年数学成绩的变化情况宜采用扇形统计图 | |
| D. | 一组数据有80分,最大值是141,最小值是60,取组距为10,可分为9组 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com