
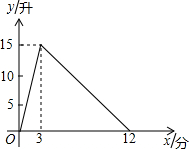
 一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.
一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.分析 ①当0≤x≤3时,设y=mx(m≠0),根据点的坐标利用待定系数法即可得出函数关系式;
②当3<x≤12时,设y=kx+b(k≠0),根据点的坐标利用待定系数法即可得出函数关系式;
③根据一次函数图象上点的坐标特征结合①②的结论,即可得出x的取值范围.
解答 解:①当0≤x≤3时,设y=mx(m≠0),
则3m=15,
解得m=5,
∴当0≤x≤3时,y与x之间的函数关系式为y=5x;
②当3<x≤12时,设y=kx+b(k≠0),
∵函数图象经过点(3,15),(12,0),
∴$\left\{\begin{array}{l}{3k+b=15}\\{12k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{5}{3}}\\{b=20}\end{array}\right.$,
∴当3<x≤12时,y与x之间的函数关系式y=-$\frac{5}{3}$x+20;
③当y=5时,由5x=5得,x=1;
由-$\frac{5}{3}$x+20=5得,x=9.
∴当容器内的水量大于5升时,时间x的取值范围是1<x<9.
点评 本题考查了一次函数的应用以及待定系数法求函数解析式,观察函数图象找出点的坐标利用待定系数法求出函数关系式是解题的关键.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:填空题
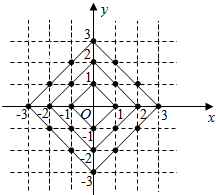 在平面直角坐标系中,横坐标、纵坐标都是整数的点称为整点,观察图中 每一个正方形(实线)四条边上的整点的个数,请你猜测出里向外第2016个正方形(实线)四条边上的整点个数共有8064个.
在平面直角坐标系中,横坐标、纵坐标都是整数的点称为整点,观察图中 每一个正方形(实线)四条边上的整点的个数,请你猜测出里向外第2016个正方形(实线)四条边上的整点个数共有8064个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
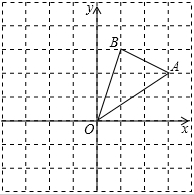 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com