
【题目】小明手中有4张背面相同的扑克牌:红桃6、红桃9、黑桃6、黑桃9.先将4张牌背面朝上洗匀,再让小丽抽牌.
(1)小丽从中任意抽取一张扑克牌,抽到黑桃9的概率是__________,抽到偶数的概率是_________;
(2)小丽从中任意抽取两张扑克牌,游戏规则规定:若小丽抽到的两张牌是一红一黑,则小丽胜,若小丽抽到的两张牌是一奇一偶,则小明胜,问该游戏对双方是否公平.(利用树状图或列表说明)
【答案】(1)![]() ,
,![]() ;(2)见解析
;(2)见解析
【解析】
(1)利用概率的求解方法即可求得;
(2)因为是两步完成的事件,所以采用列表法即可求得游戏对双方获胜的概率,概率相等则公平,否则不公平.
解:(1)小丽从中任意抽取一张扑克牌,抽到黑桃9的概率是1÷4=![]()
抽到偶数的概率是2÷4=![]()
故答案为:![]() ,
,![]() ;
;
(2)如图,
红桃6 | 红桃9 | 黑桃6 | 黑桃9 | |
红桃6 | 红桃9,红桃6 | 黑桃6,红桃6 | 黑桃9,红桃6 | |
红桃9 | 红桃6,红桃9 | 黑桃6,红桃9 | 黑桃9,红桃9 | |
黑桃6 | 红桃6,黑桃6 | 红桃9,黑桃6 | 黑桃9,黑桃6 | |
黑桃9 | 红桃6,黑桃9 | 红桃9,黑桃9 | 黑桃6,黑桃9 |
共有12种等可能结果,其中抽到的两张牌是一红一黑有8种结果,则小丽获胜的概率是![]() ;抽到的两张牌是一奇一偶有8种结果,则小明获胜的概率是
;抽到的两张牌是一奇一偶有8种结果,则小明获胜的概率是![]() ,故游戏公平.
,故游戏公平.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
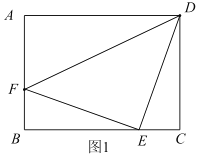
【题目】正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.
(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是 ;
(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
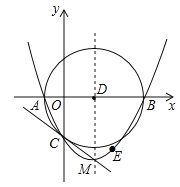
【题目】如图,抛物线y=![]() (x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
(x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,直线
,直线![]() 经过抛物线的顶点
经过抛物线的顶点![]() .已知该抛物线的对称轴为直线
.已知该抛物线的对称轴为直线![]() ,交
,交![]() 轴于点
轴于点![]() .
.
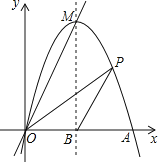
(1)求![]() 的值.
的值.
(2)![]() 是第一象限内抛物线上的一点,且在对称轴的右侧,连接
是第一象限内抛物线上的一点,且在对称轴的右侧,连接![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ;
;
①![]() 的面积为
的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
②记![]() .求
.求![]() 关于
关于![]() 的函数表达式及
的函数表达式及![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】表中所列![]() 、
、![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中![]()
| … |
|
|
|
|
|
|
| … |
| … | 6 |
| 11 |
| 11 |
| 6 | … |
根据表中提供约信息,有以下4个判断:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 的值是
的值是![]() ;④
;④![]() ;其中判断正确的是( )
;其中判断正确的是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 的顶点在
的顶点在![]() 上,
上,![]() 交直线
交直线![]() 于
于![]() 点.
点.

(1)如图1,若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
(2)如图2,![]() ,当
,当![]() 时,求证:
时,求证:![]() 是
是![]() 的中点;
的中点;
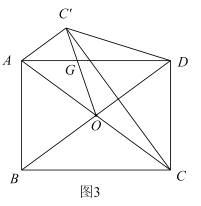
(3)如图3,若![]() ,对角线
,对角线![]() ,
,![]() 交于点
交于点![]() ,点
,点![]() 关于
关于![]() 的对称点为点
的对称点为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,求
,求![]() 的长,请直接写出答案.
的长,请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
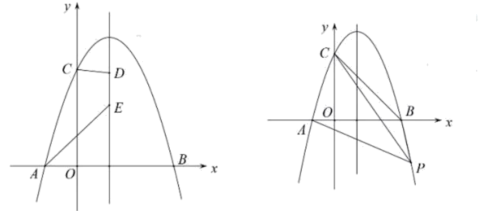
【题目】如图所示抛物线![]() 过点
过点![]() ,点
,点![]() ,且
,且![]()
(1)求抛物线的解析式及其对称轴;
(2)点![]() 在直线
在直线![]() 上的两个动点,且
上的两个动点,且![]() ,点
,点![]() 在点
在点![]() 的上方,求四边形
的上方,求四边形![]() 的周长的最小值;
的周长的最小值;
(3)点![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,直线
,直线![]() 把四边形
把四边形![]() 的面积分为3∶5两部分,求点
的面积分为3∶5两部分,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
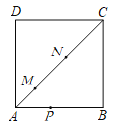
【题目】如图,在正方形ABCD中,M、N是对角线AC上的两个动点,P是正方形四边上的任意一点,且![]() ,
,![]() .关于下列结论:①当△PAN是等腰三角形时,P点有6个;②当△PMN是等边三角形时,P点有4个;③DM+DN的最小值等于6.其中,一定正确的结论的序号是_______.
.关于下列结论:①当△PAN是等腰三角形时,P点有6个;②当△PMN是等边三角形时,P点有4个;③DM+DN的最小值等于6.其中,一定正确的结论的序号是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com