
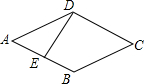
 如图,点E是菱形ABCD边上一动点,它沿A→B→C→D的路径移动,设点E经过的路径长为x,△ADE的面积为y,下列图象中能反映y与x函数关系的是( )
如图,点E是菱形ABCD边上一动点,它沿A→B→C→D的路径移动,设点E经过的路径长为x,△ADE的面积为y,下列图象中能反映y与x函数关系的是( )| A. | 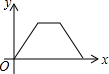 | B. | 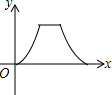 | C. | 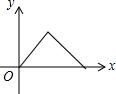 | D. | 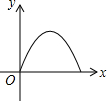 |
分析 考虑△ADE的面积变化就是要考虑当点E运动时,△ADE的底边及高的变化情况.因为点E是沿着菱形的四边运动,结合菱形性质可以知道△ADE的高都是不变的,只需要考虑底边的变化就可以了.点E在AB上移动时,底边是不断增大的;点E在BC上移动时,用AD做底边,则点的移动不会带来面积的变化;点E在CD上移动时,底边是在减少的,结合三角形面积计算公式可以得出变化趋势即得出解答.
解答 解:因为点E在菱形ABCD上移动,所以可知菱形各顶点向对边作的高为定值,可设高的长为k
如图一,当点E在AB上移动时,将AE作为△ADE底边,则有S△ADE =$\frac{1}{2}$•AE•k 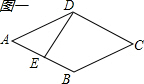
随着点E移动,AE的长在增大,三角形的面积也是在增大的,y与x满足正比例函数关系;
如图二,当点E在BC上移动时,将AD作为底边,则有S△ADE=$\frac{1}{2}$•AD•k
点E的移动不会带来AD长度的变化,所以此时三角形面积为定值;
如图三,当点E在BC上移动时,将DE作为△ADE底边,则有S△ADE=$\frac{1}{2}$•DE•k 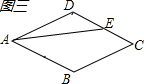
随着点E移动,DE的长在减少,三角形的面积也是在减少的,y与x满足正比例函数关系.
所以应该选A.
点评 此题主要考查了动点带来的面积变化问题,考查了分类讨论思想的应用,解答此题的关键是明确变化过程中△ADE的高是定值,学会在运动变化过程中找不变量是解决动点问题的一个核心思路.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
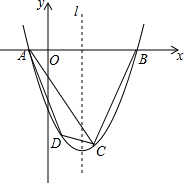 如图,已知二次函数的图象M经过A(-1,0),B(4,0),C(2,-6)三点.
如图,已知二次函数的图象M经过A(-1,0),B(4,0),C(2,-6)三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
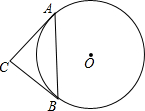 如图,已知⊙O的半径是4cm,弦AB=4$\sqrt{2}$cm,AC是⊙O的切线,切AC=4cm,连接BC.
如图,已知⊙O的半径是4cm,弦AB=4$\sqrt{2}$cm,AC是⊙O的切线,切AC=4cm,连接BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com