
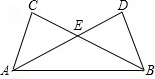
 C≌△BAD,并予以证明.
C≌△BAD,并予以证明. 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 16、如图,把边长为2cm的正方形剪成四个全等的直角三角形,请用这四个直角三角形拼成符合下列要求的图形.(全部用上,互不重合且不留空隙),并把你的拼法依照图示按实际大小画在方格内(方格为1cm×1cm)
16、如图,把边长为2cm的正方形剪成四个全等的直角三角形,请用这四个直角三角形拼成符合下列要求的图形.(全部用上,互不重合且不留空隙),并把你的拼法依照图示按实际大小画在方格内(方格为1cm×1cm)查看答案和解析>>
科目:初中数学 来源: 题型:
 24、如图,把长为2cm的正方形剪成四个全等的直角三角形,请用这四个直角三角形(全部用上)拼成下列符合要求的图形(互不重叠且没有空隙),并把你的拼法画在下列的方格纸内(方格为1cm×1cm)
24、如图,把长为2cm的正方形剪成四个全等的直角三角形,请用这四个直角三角形(全部用上)拼成下列符合要求的图形(互不重叠且没有空隙),并把你的拼法画在下列的方格纸内(方格为1cm×1cm)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A,
如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A,查看答案和解析>>
科目:初中数学 来源: 题型:
 我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题:
我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com