
【题目】某超市以20元/千克的进货价购进了一批绿色食品,如果以30元/千克销售这些绿色食品,那么每天可售出400千克.由销售经验可知,每天的销售量y(千克)与销售单价x(元)(x≥30)存在如图所示的一次函数关系.
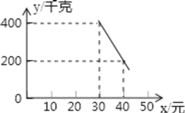
(1)试求出y与x的函数关系式;
(2)设该超市销售该绿色食品每天获得利润w元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
【答案】(1)y=﹣20x+1000(30≤x≤50);(2)当销售单价为35元/千克时,每天可获得最大利润4500元.
【解析】
(1)根据函数图象中的数据可以求得y与x的函数关系式;
(2)根据题意和(1)中的函数关系式可以求得w的最大值,从而可以解答本题.
(1)设y与x的函数关系式为y=kx+b,
![]() ,得
,得![]() ,
,
即y与x的函数关系式是y=﹣20x+1000(30≤x≤50);
(2)w=(x﹣20)y
=(x﹣20)(﹣20x+1000)
=﹣20x2+1400x﹣20000
=﹣20(x﹣35)2+4500,
故当x=35时,w取得最大值,此时w=4500,
答:当销售单价为35元/千克时,每天可获得最大利润4500元.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
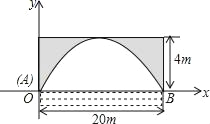
【题目】有一座抛物线形拱桥,正常水位时桥下水面宽为20m,拱顶距水面4m.
(1)在如图的直角坐标系中,求出该抛物线的解析式;
(2)为保证过往船只顺利航行,桥下水面宽度不得小于18m,求水面在正常水位基础上,最多涨多少米,不会影响过往船只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线![]() 的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
①2b﹣c=2;②a=![]() ;③ac=b﹣1;④
;③ac=b﹣1;④![]() >0
>0
其中正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践探究几何元素之间的关系
问题情境:四边形ABCD中,点O是对角线AC的中点,点E是直线AC上的一个动点(点E与点C,O,A都不重合),过点A,C分别作直线BE的垂线,垂足分别为F,G,连接OF,OG.
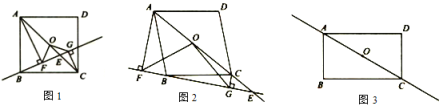
(1)初步探究:
如图1,已知四边形ABCD是正方形,且点E在线段OC上,求证![]() ;
;
(2)深入思考:请从下面A,B两题中任选一题作答,我选择_______题.
A.探究图1中OF与OG的数量关系并说明理由;
B.如图2,已知四边形ABCD为菱形,且点E在AC的延长线上,其余条件不变,探究OF与OG的数量关系并说明理由;
(3)拓展延伸:请从下面AB两题中任选一题作答,我选择_______题.
如图3,已知四边形ABCD为矩形,且![]() ,
,![]() .
.
A.点E在直线AC上运动的过程中,若![]() ,则FG的长为________.
,则FG的长为________.
B.点E在直线AC上运动的过程中,若![]() ,则FG的长为________.
,则FG的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个数的平方等于![]() ,记为
,记为![]() ,这个数
,这个数![]() 叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为![]() (
(![]() 为实数),
为实数),![]() 叫这个复数的实部,
叫这个复数的实部, ![]() 叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
例如计算: ![]()
(1)填空: ![]() =_________,
=_________, ![]() =____________.
=____________.
(2)填空:①![]() _________; ②
_________; ②![]() _________ 。
_________ 。
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知, ![]() ,(
,( ![]() 为实数),求
为实数),求![]() 的值。
的值。
(4)试一试:请利用以前学习的有关知识将![]() 化简成
化简成![]() 的形式。
的形式。
(5)解方程:x2 - 2x +4 = 0
查看答案和解析>>
科目:初中数学 来源: 题型:
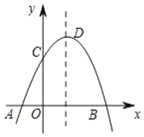
【题目】如图,抛物线y=﹣x2+2x+3交x轴于A,B两点,交y轴于点C,点D为抛物线的顶点,点C关于抛物线的对称轴的对称点为E,点G,F分别在x轴和y轴上,则四边形EDFG周长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
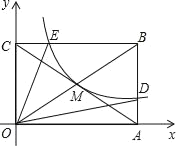
【题目】如图,反比例函数![]() (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为_____.
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com