Question

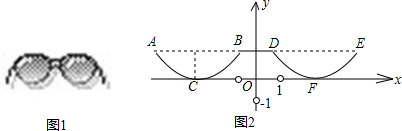
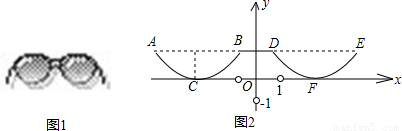
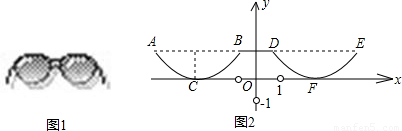
如图①是一张眼镜的照片，两镜片下半部分轮廓可以近似看成抛物线形状．建立如图②直角坐标系，已知左轮廓线端点A、B间的距离为4cm，点A、B与右轮廓线端点D、E均在平行于x轴的直线上，最低点C在x轴上，且与AB的距离CH=1cm，y轴平分BD，BD=2cm．解答下列问题：
（1）求轮廓线ACB的函数解析式；（写出自变量x的取值范围）
（2）由（1）写出右轮廓线DFE对应的函数解析式及自变量x的取值范围．

Answer 1

分析：（1）易得A、B、C三点的坐标，根据待定系数法就可以求出抛物线的解析式；
（2）轮廓线DFE是抛物线．F是顶点，并且经过点D、E，根据待定系数法就可求出抛物线的解析式．

解答：解：（1）设左轮廓线ACB的抛物线解析式为y=ax²+bx+c（a≠0）（1分）
∵A（-5，1），B（-1，1），C（-3，0）
∴

25a-5b+c=1 a-b+c=1 9a-3b+c=0

解得：

a= 1 4 b= 3 2 c= 9 4

；
∴左轮廓线ACB的抛物线解析式为：y=

1

4

x²+

3

2

x+

9

4

（-5≤x≤-1）（9分）；

（2）由左右两轮廓线关于y轴对称，
又y=

1

4

（x+3）²，顶点C（-3，0），
∴顶点C关于y轴对称点F（3，0）且a₁=

1

4

，
∴右轮廓线DFE对应的函数解析式为y=

1

4

（x-3）²，即：y=

1

4

x²-

3

2

x+

9

4

（1≤x≤5）．（12分）

点评：本题主要考查了待定系数法求抛物线的解析式，难易程度适中．