
【题目】如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为( ) 
A.![]()
B.3 ![]()
C.5
D.6
【答案】C
【解析】解:∵四边形ABCD是正方形,AC为对角线, ∴∠EAF=45°,
又∵EF⊥AC,
∴∠AFE=90°,∠AEF=45°,
∴EF=AF=3,
∵△EFC的周长为12,
∴FC=12﹣3﹣EC=9﹣EC,
在Rt△EFC中,EC2=EF2+FC2 ,
∴EC2=9+(9﹣EC)2 ,
解得EC=5.
所以答案是:5.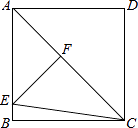
【考点精析】通过灵活运用勾股定理的概念和正方形的性质,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
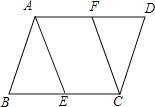
A. AF=CE B. AE=CF C. ∠BAE=∠FCD D. ∠BEA=∠FCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.
(1)当m= ![]() 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;
(2)当m>1时,连接CA,当CA⊥CP时,求m的值;
(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E恰好落在坐标轴上?若存在,请直接写出所有满足条件的点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两所学校共82人参加文艺汇演(其中甲校人数多于乙校人数,且甲校人数小于80人),如果两所学校分别购买服装,共付款6060元.
购买服装套数 | 1~40 | 41~80 | 81套及81套以上 |
每套服装价格 | 80元 | 70元 | 60元 |
(1)如果甲、乙两所学校联合起来购买服装,那么比各自购买服装一共可以节约多少钱?
(2)甲、乙两所学校各有多少学生参加演出?
(3)如果乙学校单独购买时,服装厂每件服装获利60%,丙学校购买的服装比乙多15套,那么服装厂卖给丙学校服装时共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.

(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com