
 如图,在正方形ABCD中,对角线AC、BD相交于点O点,EF为BC边上的两点,且∠EOF=45°,过点O作OE的垂线OG,交AB于点G,连接FG,下列结论:①△COE≌△BOG;②△COE∽△BOF;③CE+BF=EF;④CE2+BF2=EF2.其中正确结论的序号是①④(把正确结论的序号都填在横线上)
如图,在正方形ABCD中,对角线AC、BD相交于点O点,EF为BC边上的两点,且∠EOF=45°,过点O作OE的垂线OG,交AB于点G,连接FG,下列结论:①△COE≌△BOG;②△COE∽△BOF;③CE+BF=EF;④CE2+BF2=EF2.其中正确结论的序号是①④(把正确结论的序号都填在横线上) 分析 如图,作辅助线;首先运用正方形的性质证明OB=OC,∠OBG=∠OCE=45°;证明∠BOG=∠COE,运用ASA公理即可证明△COE≌△BOG,得到结论①正确;证明△MOE≌△COE,得到∠OME=∠OCE=45°,进而得到∠EMF=90°,运用勾股定理即可证明结论④正确.
解答 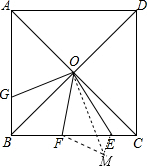 解:如图,作△OBF的对称△OMF,连接ME;
解:如图,作△OBF的对称△OMF,连接ME;
∵四边形ABCD为正方形,
∴OB=OC,∠OBG=∠OCE=45°,∠BOC=90°;
∵OG⊥OE,
∴∠BOG=∠COE;在△COE与△BOG中,
$\left\{\begin{array}{l}{∠COE=∠BOG}\\{OC=OB}\\{∠OBG=∠OCE}\end{array}\right.$,
∴△COE≌△BOG(ASA),
故①正确.
设∠BOF=α,∠COE=β;
∵∠BOC=90°,∠EOF=45°,
∴α+β=90°-45°=45°;
由题意得:∠MOF=∠BOF=α,∠OMF=∠OBF=45°,
OM=OB;则∠MOE=45°-α,OC=OM;
∵∠COE=45°-α,
∴∠MOE=∠COE;在△MOE与△COE中,
$\left\{\begin{array}{l}{OC=OM}\\{∠COE=∠MOE}\\{OE=OE}\end{array}\right.$,
∴△MOE≌△COE(SAS),
∴ME=CE,∠OME=∠OCE=45°,
∴∠FME=90°,MF2+ME2=EF2,
即CE2+BF2=EF2,
故④正确,
故答案为①④.
点评 该题主要考查了正方形的性质、全等三角形的判定、勾股定理等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用正方形的性质、全等三角形的判定、勾股定理等几何知识点来分析、判断、推理或解答.


科目:初中数学 来源: 题型:选择题
| A. | ∠A=∠B,∠C=∠D | B. | AB∥CD,AD=BC | C. | AB∥CD,∠A=∠C | D. | AO=BO,CO=DO |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $2\sqrt{3}×3\sqrt{3}=6\sqrt{3}$ | B. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C. | $5\sqrt{5}-2\sqrt{2}=3\sqrt{3}$ | D. | $\sqrt{{{(-3)}^2}}=3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2xy,2xy | B. | -2xy,-2xy | C. | 2xy,-2xy | D. | 2xy,2xy |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 车库的电动门栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD的大小是( )
车库的电动门栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD的大小是( )| A. | 150° | B. | 180° | C. | 270° | D. | 360° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,平面直角坐标系中,矩形ABCD的顶点A的坐标(3,6),AB=6,AD=3,将矩形向下平移m个单位,使矩形的两个顶点恰好同时落在某个反比例函数的图象上,则m=$\frac{3}{2}$或$\frac{15}{2}$.
如图,平面直角坐标系中,矩形ABCD的顶点A的坐标(3,6),AB=6,AD=3,将矩形向下平移m个单位,使矩形的两个顶点恰好同时落在某个反比例函数的图象上,则m=$\frac{3}{2}$或$\frac{15}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com