【题目】“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70km/h．如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处，过了2s后，测得小汽车与车速检测仪间距离为50m，这辆小汽车超速了吗？（参考数据转换：1m/s=3.6km/h）
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案科目：初中数学 来源： 题型：
【题目】数学问题：计算
（其中m，n都是正整数，且m≥2，n≥1）．
探究问题：为解决上面的数学问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究．
探究一：计算
．
第1次分割，把正方形的面积二等分，其中阴影部分的面积为
；
第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为
；
第3次分割，把上次分割图中空白部分的面积继续二等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为
，最后空白部分的面积是
．
根据第n次分割图可得等式： 
=1﹣
．
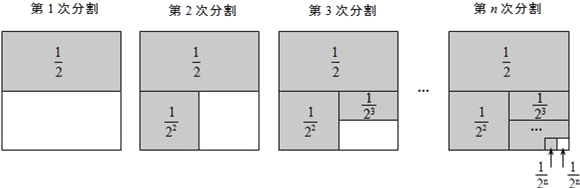
探究二：计算
．
第1次分割，把正方形的面积三等分，其中阴影部分的面积为
；
第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为
；
第3次分割，把上次分割图中空白部分的面积继续三等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为
，最后空白部分的面积是
．
根据第n次分割图可得等式： 
=1﹣
，
两边同除以2，得
=
.
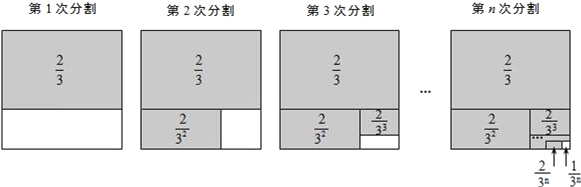
探究三：计算
．
（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）
解决问题：计算
．
（只需画出第n次分割图，在图上标注阴影部分面积，并完成以下填空）
根据第n次分割图可得等式： ，
所以， 
= ．
拓广应用：计算
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两人分别从相距30千米的A、B两地同时相向而行，经过3小时后相距3千米，再经过2小时，甲到B地所剩的路程是乙到A地所剩路程的2倍，试求甲、乙两人的速度.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将正n边形绕点A顺时针旋转60°后，发现旋转前后两图形有另一交点O，连接AO，我们称AO为“叠弦”；再将“叠弦”AO所在的直线绕点A逆时针旋转60°后，交旋转前的图形于点P，连接PO，我们称∠OAB为“叠弦角”，△AOP为“叠弦三角形”．
【探究证明】
（1）请在图1和图2中选择其中一个证明：“叠弦三角形”（△AOP）是等边三角形；
（2）如图2，求证：∠OAB=∠OAE′．
【归纳猜想】
（3）图1、图2中的“叠弦角”的度数分别为 ， ；
（4）图n中，“叠弦三角形” 等边三角形（填“是”或“不是”）
（5）图n中，“叠弦角”的度数为 （用含n的式子表示）
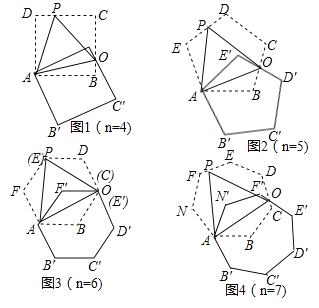
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】证明命题“直角三角形中的两个锐角中至少有一个角不小于45°”时，如果用反证法证明，应先假设__________________________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
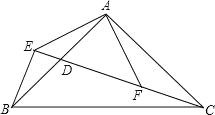
【题目】如图，在△ABC中，∠BAC=90°，AB=AC，点D是AB的中点，连接CD，过B作BE⊥CD交CD的延长线于点E，连接AE，过A作AF⊥AE交CD于点F．
（1）求证：AE=AF；
（2）求证：CD=2BE+DE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E，F．
⑴试说明：BE=CF；
⑵若AF=3，BC=4，求△ABC的周长．
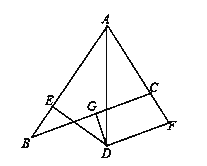
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一副直角三角板按图11-14摆放，点C在EF上，AC经过点D．已知∠A=∠EDF=90°，AB=AC，∠E=30°，∠BCE=40°.求∠CDF的度数.
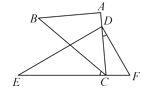
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
