
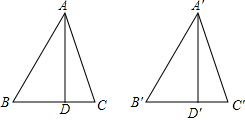
 如图,锐角△ABC和锐角△A′B′C′中,AD,A′D′分别是BC,B′C′上的高,且AB=A′B′,AD=A′D′.要使△ABC≌△A′B′C′,则应补充的条件是CD=C′D′(或AC=A′C′,或∠C=∠C′或∠CAD=∠C′A′D′)答案不唯一(填写一个即可).
如图,锐角△ABC和锐角△A′B′C′中,AD,A′D′分别是BC,B′C′上的高,且AB=A′B′,AD=A′D′.要使△ABC≌△A′B′C′,则应补充的条件是CD=C′D′(或AC=A′C′,或∠C=∠C′或∠CAD=∠C′A′D′)答案不唯一(填写一个即可). 分析 根据判定方法,结合图形和已知条件,寻找添加条件.
解答 解:我们可以先利用HL判定△ABD≌△A′B′D′得出对应边相等,对应角相等.
此时若添加CD=C?D?,可以利用SAS来判定其全等;
添加∠C=∠C?,可以利用AAS判定其全等;
还可添加AC=A′C′,∠CAD=∠C′A′D′等.
故答案为CD=C′D′(或AC=A′C′,或∠C=∠C′或∠CAD=∠C′A′D′)答案不唯一.
点评 本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{{x}^{2}}{4}$+1 | B. | y=x2+2x+1 | C. | y=2x2+1 | D. | y=x2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
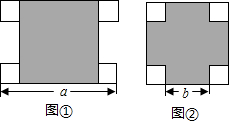 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是(用含a、b的式子表示)( )
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是(用含a、b的式子表示)( )| A. | (a+b)2 | B. | (a-b)2 | C. | 2ab | D. | ab |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
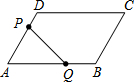 如图,在平行四边形ABCD中,AB=8cm,AD=4cm,∠A=60°,动点P以2cm/s的速度从D向点A移动,动点Q以4cm/s的速度从点A向点B移动.如果P、Q两点分别从D、A同时出发,当一方到达终点时都随之停止运动,那么经过1秒,五边形PQBCD面积最小.
如图,在平行四边形ABCD中,AB=8cm,AD=4cm,∠A=60°,动点P以2cm/s的速度从D向点A移动,动点Q以4cm/s的速度从点A向点B移动.如果P、Q两点分别从D、A同时出发,当一方到达终点时都随之停止运动,那么经过1秒,五边形PQBCD面积最小.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com