
����Ŀ����ʡij��������һ����ɫ�߲ˣ����г�����ֱ�����ۣ�ÿ������Ϊ1000Ԫ�����ּӹ������ۣ�ÿ������ɴ�4500Ԫ�������ӹ������ۣ�ÿ����������7500Ԫ�� ����һ��ũ���̹�˾�ջ������߲�140�֣��ù�˾�ӹ��������������ǣ�������߲˽��дּӹ���ÿ��ɼӹ�16�֣�������о��ӹ���ÿ��ɼӹ�6�֣������ּӹ���ʽ����ͬʱ���У��ܼ��ڵ��������ƣ���˾������15���ʱ�佫�����߲�ȫ�����ۻ�ӹ���ϣ�Ϊ�ˣ���˾���������ֿ��з�����
����һ�����߲�ȫ�����дּӹ���
�������������ܶ�Ķ��߲˽��о��ӹ���û���ü����мӹ����߲ˣ����г���ֱ�ӳ��ۣ�
����������һ�����߲˽��о��ӹ��������߲˽��дּӹ�����ǡ����15����ɣ�
����Ϊѡ�����ַ���������ࣿΪʲô��
���𰸡��⣺ѡ������ַ���������࣮ ����һ����Ϊÿ��ּӹ�16�֣�140�ֿ�����15���ڼӹ��꣮
������W1=4500��140=630000��Ԫ��
����������Ϊÿ�쾫�ӹ�6�֣�15����Լӹ�90�֣�����50��ֱ�����ۣ�
������W2=90��7500+50��1000=725000��Ԫ��
����������15���ھ��ӹ��߲�x�֣��ּӹ��߲�y�֣�������� 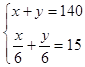 �����
����� ![]()
������W3=60��7500+80��4500=810000��Ԫ��
�ۺ��������ַ��������������֪W1��W2��W3 �� ���Ե����ַ���������࣮��8�֣�
��������Ҫ�ж���һ�ַ���������ֻ࣬Ҫ���ÿ�ַ����������٣��ٽ��бȽϾͿ����ˣ������ַ������ж��ٴּӹ����ж���ϸ�ӹ���Ҫ�ж�Ԫһ�η������������


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AB=6cm��BC=12cm����P�ӵ�A��������AB�����B��ÿ��1cm���ٶ��ƶ���ͬʱ��Q�ӵ�B������BC�����C��ÿ��2cm���ٶ��ƶ�P��Q�����ڷֱ�B��C������ֹͣ�ƶ����������ƶ���ʱ��Ϊt�룬�ش��������⣺
��1����ͼ1����tΪ����ʱ����PBQ���������5cm2��
��2����ͼ2����t=![]() ��ʱ�����ж���DPQ����״����˵�����ɣ�
��ʱ�����ж���DPQ����״����˵�����ɣ�
��3����ͼ3����QΪԲ�ģ�PQΪ�뾶����Q��
�����˶������У��Ƿ����������tֵ��ʹ��Q�������ı���DPQC��һ�ߣ�������ڵ�ֱ�ߣ����У������ڣ����tֵ���������ڣ���˵�����ɣ�
������Q���ı���DPQC�����������㣬��ֱ��д��t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м������У�ͬһ�������������ͼ��ȫ��ͬ���ǣ� ��
A.��
B.Բ
C.Բ��
D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������A�����һ����¥����B�ĸ���Ϊ23�㣬����ⶰ��¥�ײ�C�ĸ���Ϊ45�㣮��֪������A�������ĸ߶�Ϊ180m�����ⶰ��¥�ĸ߶ȣ���ȷ��1m�������ο����ݣ�sin23��=0.39��cos23��=0.92��tan23��=0.42��
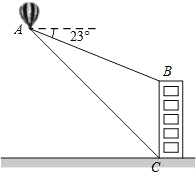
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=kx+b��k��b�dz�����k��0����ͼ����ͼ��ʾ����ʽkx+b��0�Ľ⼯�ǣ�������
A. x��-2 B. x��0 C. x��-2 D. x��0
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com