
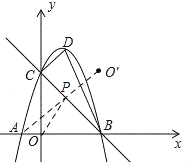
【题目】如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.

【答案】(1)y=﹣x2+2x+3;(2)P (![]() ,
,![]() );(3)当Q的坐标为(0,0)或(9,0)时,以A、C、Q为顶点的三角形与△BCD相似.
);(3)当Q的坐标为(0,0)或(9,0)时,以A、C、Q为顶点的三角形与△BCD相似.
【解析】
(1)先求得点B和点C的坐标,然后将点B和点C的坐标代入抛物线的解析式得到关于b、c的方程,从而可求得b、c的值;(2)作点O关于BC的对称点O′,则O′(3,3),则OP+AP的最小值为AO′的长,然后求得AO′的解析式,最后可求得点P的坐标;(3)先求得点D的坐标,然后求得CD、BC、BD的长,依据勾股定理的逆定理证明△BCD为直角三角形,然后分为△AQC∽△DCB和△ACQ∽△DCB两种情况求解即可.
(1)把x=0代入y=﹣x+3,得:y=3,
∴C(0,3).
把y=0代入y=﹣x+3得:x=3,
∴B(3,0),A(﹣1,0).
将C(0,3)、B(3,0)代入y=﹣x2+bx+c得:![]() ,解得b=2,c=3.
,解得b=2,c=3.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)如图所示:作点O关于BC的对称点O′,则O′(3,3).
∵O′与O关于BC对称,
∴PO=PO′.
∴OP+AP=O′P+AP≤AO′.
∴OP+AP的最小值=O′A=![]() =5.
=5.
O′A的方程为y=![]()
P点满足 解得:
解得:
所以P (![]() ,
,![]() )
)
(3)y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4).
又∵C(0,3,B(3,0),
∴CD=![]() ,BC=3
,BC=3![]() ,DB=2
,DB=2![]() .
.
∴CD2+CB2=BD2,
∴∠DCB=90°.
∵A(﹣1,0),C(0,3),
∴OA=1,CO=3.
∴![]() .
.
又∵∠AOC=DCB=90°,
∴△AOC∽△DCB.
∴当Q的坐标为(0,0)时,△AQC∽△DCB.
如图所示:连接AC,过点C作CQ⊥AC,交x轴与点Q.

∵△ACQ为直角三角形,CO⊥AQ,
∴△ACQ∽△AOC.
又∵△AOC∽△DCB,
∴△ACQ∽△DCB.
∴![]() ,即
,即![]() ,解得:AQ=10.
,解得:AQ=10.
∴Q(9,0).
综上所述,当Q的坐标为(0,0)或(9,0)时,以A、C、Q为顶点的三角形与△BCD相似.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,若∠BAC=30°,且∠ECF=∠E.
(1)试判断CF与⊙O的位置关系,并说明理由;
(2)设⊙O的半径为2,且AC=CE,求AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;(2)若∠PAC=20°,求∠AEB的度数;
(3)连结CE,写出AE, BE, CE之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b>0;③b2﹣4ac>0;④a﹣b+c>0,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一款进价为每件40元的护肤品,调查发现,销售单价不低于40元且不高于80元时,该商品的日销售量y(件)与销售单价x(元)之间存在一次函数关系,当销售单价为44元时,日销售量为72件;当销售单价为48元时,日销售量为64件.
(1)求y与x之间的函数关系式;
(2)设该护肤品的日销售利润为w(元),当销售单价x为多少时,日销售利润w最大,最大日销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知D,E分别为边BC,AD的中点,且S△ABC=4 cm2,则△BEC的面积为( )

A. 2 cm2 B. 1 cm2 C. 0.5 cm2 D. 0.25 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雪枫中学食堂一工人在每天摆碗的过程中总结出,如果你给他报出桌面上碗的高度,他能说出碗的个数,你给他报出碗的个数他能说出确的高度,真可谓数学就在身边,缺乏慧眼发现:

(1)求整齐叠放在桌面上碗的高度y(cm)与碗数x(个)之间的一次函数解析式(不要求写出自变量 x的取值范围):
(2)若桌面上有12个碗,整齐叠放成一摞,求出它的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出问题:一口袋装有除颜色外均相同的2个红球1个白球和1个篮球,小刚和小明想通过摸球来决定谁去看电影,同学甲设计了如下的方案:第一次随机从口袋中摸出一球(不放回);第二次再任意摸出一球,两人胜负规则如下:摸到“一红一白”,则小刚看电影;摸到“一白一蓝”,则小明看电影.
(1)同学甲的方案公平吗?请用列表或画树状图的方法说明;
(2)你若认为这个方案不公平,那么请你改变一下规则,设计一个公平的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△AOB是边长为2的等边三角形,将△AOB绕着点B按顺时针方向旋转得到△DCB,使得点D落在x轴的正半轴上,连接OC,AD.
(1)求证:OC=AD;
(2)求OC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com