
分析 分析:①先化简$\sqrt{50}=5\sqrt{2},\sqrt{18}=3\sqrt{2},\sqrt{\frac{1}{2}}=\frac{1}{2}\sqrt{2}$,最后合并同类二次根式;②运用平方式公式化简$(3+\sqrt{3})(3-\sqrt{3})={3}^{2}-(\sqrt{3})^{2}$=6,再化简$\frac{\sqrt{8}+\sqrt{6}}{\sqrt{2}}=\frac{\sqrt{8}}{\sqrt{2}}+\frac{\sqrt{6}}{\sqrt{2}}$=$\sqrt{4}-\sqrt{3}$=2-$\sqrt{3}$,最后合并同类二次根据求解.
解答 解:①$\sqrt{50}+\sqrt{18}-\sqrt{\frac{1}{2}}$,
=$5\sqrt{2}+3\sqrt{2}-\frac{1}{2}\sqrt{2}$,
=(5+3-$\frac{1}{2}$)$\sqrt{2}$,
=$\frac{15}{2}$$\sqrt{2}$.
②(3+$\sqrt{3}$)(3-$\sqrt{3}$)+$\frac{{\sqrt{8}+\sqrt{6}}}{{\sqrt{2}}}$
=${3}^{2}-{(\sqrt{3})}^{2}$+$\frac{\sqrt{8}}{\sqrt{2}}+\frac{\sqrt{6}}{\sqrt{2}}$,
=9-3+2+$\sqrt{3}$,
=8+$\sqrt{3}$.
点评 本题考查的是二次根式的加减运算,其实质是二并同类二次根式.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A、B、C在⊙O上,∠AOB=150°,∠ABC=45°,延长OB到D,使BD=OB,连结CD.
如图,点A、B、C在⊙O上,∠AOB=150°,∠ABC=45°,延长OB到D,使BD=OB,连结CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,P是AD上一点,E为BP上一点,且AE=BE=EP,
如图,平行四边形ABCD中,P是AD上一点,E为BP上一点,且AE=BE=EP,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
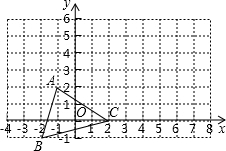 如图,已知在平面直角坐标系中,△ABC的位置如图所示.
如图,已知在平面直角坐标系中,△ABC的位置如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com