
【题目】四边形![]() 是由等边
是由等边![]() 和顶角为120°的等腰三角形
和顶角为120°的等腰三角形![]() 拼成,将一个60°角顶点放在点
拼成,将一个60°角顶点放在点![]() 处,60°角两边分别交直线
处,60°角两边分别交直线![]() 于
于![]() ,交直线
,交直线![]() 于
于![]() 两点.
两点.
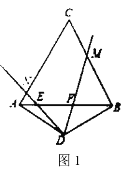
(1)当![]() 都在线段
都在线段![]() 上时,探究
上时,探究![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
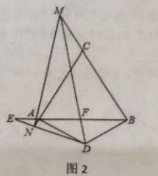
(2)当![]() 在边
在边![]() 的延长线上时,求证:
的延长线上时,求证:![]() .
.
【答案】(1)BM+AN=MN,证明见解析;(2)见解析;
【解析】
(1)把△DBM绕点D逆时针旋转120°得到△DAQ,根据旋转的性质可得DM=DQ,AQ=BM,∠ADQ=∠BDM,然后求出∠QDN=∠MDN,利用“边角边”证明△MND和△QND全等,根据全等三角形对应边相等可得MN=QN,再根据AQ+AN=QN整理即可得证;
(2)把△DAN绕点D顺时针旋转120°得到△DBP,根据旋转的性质可得DN=DP,AN=BP,根据∠DAN=∠DBP=90°可知点P在BM上,然后求出∠MDP=60°,然后利用“边角边”证明△MND和△MPD全等,根据全等三角形对应边相等可得MN=MP,从而得证;
(1)证明:∵四边形![]() 是由等边
是由等边![]() 和顶角为120°的等腰三角形
和顶角为120°的等腰三角形![]() 拼成,
拼成,
∴∠CAD=∠CBD=60°+30°=90°
把△DBM绕点D逆时针旋转120°得到△DAQ,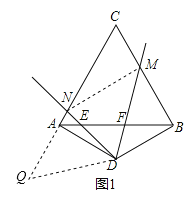
则DM=DQ,AQ=BM,∠ADQ=∠BDM,∠CBD=∠QAD =90°
∴∠CAD+∠QAD =180°
∴N、A、Q三点共线
∵∠QDN=∠ADQ+∠ADN=∠BDM+∠ADN=∠ABD-∠MDN=120°-60°=60°,
∴∠QDN=∠MDN=60°,
∵在△MND和△QND中,
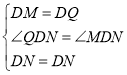
∴MN=QN,
∵QN=AQ+AN=BM+AN,
∴BM+AN=MN;
(2)MN+AN=BM.
理由如下:如图,把△DAN绕点D顺时针旋转120°得到△DBP,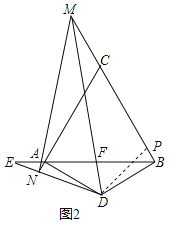
则DN=DP,AN=BP,
∵∠DAN=∠DBP=90°,
∴点P在BM上,
∵∠MDP=∠ADB-∠ADM-∠BDP=120°-∠ADM-∠ADN=120°-∠MDN=120°-60°=60°,
∴∠MDP=∠MDN=60°,
∵在△MND和△MPD中,

∴△MND≌△MPD(SAS),
∴MN=MP,
∵BM=MP+BP,
∴MN+AN=BM;
∴MN=BM -AN;


科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年 3 月 12 日植树节期间, 学校预购进 A、B 两种树苗,若购进 A种树苗 3 棵,B 种树苗 5 棵,需 2100 元,若购进 A 种树苗 4 棵,B 种树苗 10棵,需 3800 元.
(1)求购进 A、B 两种树苗的单价;
(2)若该单位准备用不多于 8000 元的钱购进这两种树苗共 30 棵,求 A 种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是直线
是直线![]() 上一点,以
上一点,以![]() 为一边在
为一边在![]() 的右侧作等边
的右侧作等边![]() .
.
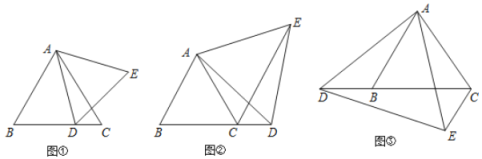
(1)如图①,点![]() 在线段
在线段![]() 上移动时,直接写出
上移动时,直接写出![]() 和
和![]() 的大小关系;
的大小关系;
(2)如图②,点![]() 在线段
在线段![]() 的延长线上移动时,猜想
的延长线上移动时,猜想![]() 的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC

①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据以下10个乘积,回答问题:
11×29;12×28;13×27;14×26;15×25;16×24;17×23;18×22;19×21;20×20.
(1)将以上各乘积分别写成“a2﹣b2”(两数平方)的形式,将以上10个乘积按照从小到大的顺序排列起来;
(2)用含有a,b的式子表示(1)中的一个一般性的结论(不要求证明);
(3)根据(2)中的一般性的结论回答下面问题:某种产品的原料提价,因而厂家决定对产品进行提价,现有两种方案方案:第一次提价p%,第二次提价q%;方案2:第一、二次提价均为![]() %,其中p≠q,比较哪种方案提价最多?
%,其中p≠q,比较哪种方案提价最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的位似比为1:2,画出△A1B1C1(△ABC与△A1B1C1在位似中心O点的两侧,A,B,C的对应点分别是A1,B1,C1).
(2)利用方格纸标出△A1B1C1外接圆的圆心P,P点坐标是 ,⊙P的半径= .(保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
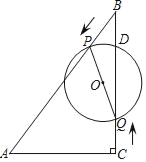
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6cm,∠ABC=30°,动点P从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒![]() cm的速度向点B匀速运动,运动时间为t秒(0≤t≤6),连接PQ,以PQ为直径作⊙O.
cm的速度向点B匀速运动,运动时间为t秒(0≤t≤6),连接PQ,以PQ为直径作⊙O.
(1)当t=1时,求△BPQ的面积;
(2)设⊙O的面积为y,求y与t的函数解析式;
(3)若⊙O与Rt△ABC的一条边相切,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com