
【题目】如图,已知反比例函数y1=![]() 与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
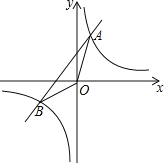
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() x+b的解.
x+b的解.
【答案】(1)k1=8,k2=2,b=6(2)15(3)-4≤x<0或x≥1
【解析】试题分析:(1)将A点的坐标代入反比例函数的解析式,可得出反比例函数解析式,再结合点B的横坐标即可得出点B的坐标,根据点A、B的坐标利用待定系数法即可求出一次函数的解析式;
(2)先求出一次函数图像与y轴的交点坐标,再将△AOB的面积分成两个小三角形面积分别求解即可;
(3)根据两函数图像的上下位置关系即可得出不等式的解集.
试题解析:(1)∵反比例函数y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m),
与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m),
∴k1=1×8=8,m=8÷(-4)=-2,
∴点B的坐标为(-4,-2).
将A(1,8)、B(-4,-2)代入y2=k2x+b中, ![]() ,解得:
,解得: ![]() .
.
∴k1=8,k2=2,b=6.
(2)当x=0时,y2=2x+6=6,
∴直线AB与y轴的交点坐标为(0,6).
∴S△AOB=![]() ×6×4+
×6×4+![]() ×6×1=15.
×6×1=15.
(3)观察函数图象可知:当-4<x<0或x>1时,一次函数的图象在反比例函数图象的上方,
∴不等式![]() x+b的解为-4≤x<0或x≥1.
x+b的解为-4≤x<0或x≥1.


科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800平方米区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400平方米区域绿化时,甲队比乙队少用4天.求甲、乙两工程队每天能完成绿化的面积分别是多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
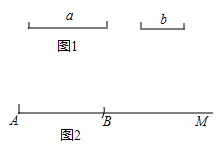
【题目】阅读材料:用尺规作图要求作线段AB等于线段a时,小明的具体作法如下:
已知:线段a,如图1
求作:线段AB,使得线段AB=a.
解:作图步骤如下:
①作射线AM;
②用圆规在射线AM上截取AB=a,如图2.
∴线段AB为所求作的线段.
解决下列问题:
已知:线段b,如图1
(1)请你依照小明的作法,在上图②中的射线AB作线段BD,使BD=b;(不要求写作法和结论,保留作图痕迹,用签字笔加粗)
(2)在(1)的条件下,取AD的中点E,若AB=3,BD=2,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把二次函数y=﹣(x+1)2﹣3的图象沿着x轴翻折后,得到的二次函数有( )
A.最大值y=3B.最大值y=﹣3C.最小值y=3D.最小值y=﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)).图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3 . 若正方形EFGH的边长为2,则S1+S2+S3= . 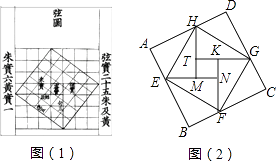
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的数为a,点B表示的数为b,且a,b满足|a+2|+(3a+b)2=0,O为原点.
![]()
(1)则a= ,b= ;
(2)若动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,
①当PO=2PB时,求点P的运动时间t;
②当点P运动到线段OB上时,分别取AP和OB的中点E、F,则![]() 的值是否为一个定值?如果是,求出定值,如果不是,说明理由.
的值是否为一个定值?如果是,求出定值,如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
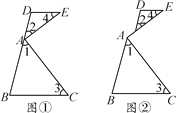
【题目】如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com