
【题目】已知A(1,0)、B(0,-1)、C(-1,2)、D(2,-1)、E(4,2)五个点,抛物线y=a(x-1)2+k(a>0)经过其中的三个点.
(1)求证:C、E两点不可能同时在抛物线y=a(x-1)2+k(a>0)上;
(2)点A在抛物线y=a(x-1)2+k(a>0)上吗?为什么?
(3)求a和k的值.
【答案】
(1)
解:∵抛物线y=a(x-1)2+k的对称轴为x=1,
而C(-1,2),E(4,2)两点纵坐标相等,
由抛物线的对称性可知,C、E关于直线x=1对称,
又∵C(-1,2)与对称轴相距2,E(4,2)与对称轴相距3,
∴C、E两点不可能同时在抛物线上;
(2)
解:假设点A(1,0)在抛物线y=a(x-1)2+k(a>0)上,
则a(1-1)2+k=0,解得k=0,
因为抛物线经过5个点中的三个点,
将B(0,-1)、C(-1,2)、D(2,-1)、E(4,2)代入,
得出a的值分别为a=-1,a= ![]() ,a=-1,a=
,a=-1,a= ![]() ,
,
所以抛物线经过的点是B,D,
又因为a>0,与a=-1矛盾,
所以假设不成立.
所以A不在抛物线上;
而k为任意数,这与抛物线是确定的矛盾,故点A不在抛物线y=a(x-1)2+k(a>0)上.
∴A点不在抛物线上
(3)
解:将D(2,-1)、C(-1,2)两点坐标代入y=a(x-1)2+k中,得
![]() 解得
解得![]()
或将E、D两点坐标代入y=a(x-1)2+k中,得 |
![]() 解得
解得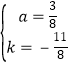
综上所述,
![]()
或 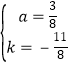
【解析】本题考查了二次函数图象上点的坐标特点.关键是明确图象上点的坐标必须满足函数解析式.(1)由抛物线y=a(x-1)2+k可知,抛物线对称轴为x=1,而C(-1,2),E(4,2)两点纵坐标相等,应该关于直线x=1对称,但C(-1,2)与对称轴相距2,E(4,2)与对称轴相距3,故不可能;(2)假设A点在抛物线上,得出矛盾排除A点在抛物线上;(3)B、D两点关于对称轴x=1对称,一定在抛物线上,另外一点可能是C点或E点,分别将C、D或D、E两点坐标代入求a和k的值.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】为提高居民的节水意识,向阳小区开展了“建设节水型社区,保障用水安全”为主题的节水宣传活动.小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查.她在300户家庭中随机调查了50户家庭5月份的用水量,结果如图所示.把图中每组用水量的值用该组的中间值(如0~6的中间值为3)来代替,估计该小区5月份的用水量.
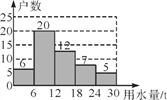
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从图![]() 所示的风筝中可以抽象出几何图形,我们把这种几何图形叫做“筝形”.
所示的风筝中可以抽象出几何图形,我们把这种几何图形叫做“筝形”.
具体定义如下:如图![]() ,在四边形
,在四边形![]() 中,
中, ![]() ,
, ![]() ,我们把这种两组邻边分别相等的四边形叫做“筝形”.
,我们把这种两组邻边分别相等的四边形叫做“筝形”.

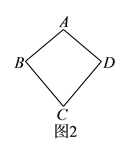
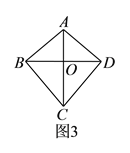
(![]() )结合图
)结合图![]() ,通过观察、测量、折纸,可以猜想“筝形”具有诸如“
,通过观察、测量、折纸,可以猜想“筝形”具有诸如“![]() 平分
平分![]() 和
和![]() ”这样的性质,请结合图形,再写出两条“筝形”的性质.
”这样的性质,请结合图形,再写出两条“筝形”的性质.
①____________________________.
②____________________________.
(![]() )从你写出的两条性质中,任选一条“筝形”的性质给出证明.
)从你写出的两条性质中,任选一条“筝形”的性质给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,完全平方式可以用平面几何图形的面积来表示。实际上还有一些代数恒等式也可以用这种形式表示,如:(2a+b)(a+b)=2a2+3ab+b2,就可以用图(1)或图(2)等图形的面积表示。

(1)请写出图(3)所表示的代数恒等式: ;
(2)试画一个几何图形,使它的面积表示:(a+b)(a+2b)=a2+3ab+2b2;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在如图所示的平面直角中, 将其平移后得△![]() , 若B的对应点
, 若B的对应点![]() 的坐标是(-2, 2).
的坐标是(-2, 2).
(1) 在图中画出△![]() ;
;
(2) 此次平移可看作将△ABC向_____平移了____个单位长度, 再向___平移了___个单位长度得△![]() ;
;
(3) △ABC的面积为____________.(△ABC的面积可以看作一个长方形的面积减去一些小三角形的面积)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探究 探索:在如图1至图3中,△ABC的面积为a .
(1)如图1, 延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1,则S1=________(用含a的代数式表示);




(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则S2= (用含a的代数式表示);
(3)在图2的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3=__________(用含a的代数式表示).
发现:像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的_____倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x-2)(x-3)=m有实数根x1、x2 , 且x1≠x2 , 有下列结论:①x1=2,x2=3;②m> ![]() ;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是( )
;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有凫(凫:野鸭)起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海.野鸭与大雁从南海和北海同时起飞,经过几天相遇.设野鸭与大雁从南海和北海同时起飞,经过x天相遇,根据题意,下面所列方程正确的是( )
A. (9-7)x=1 B. (9-7)x=1 C. (![]() +
+![]() )x=1 D. (
)x=1 D. (![]() -
-![]() )x=1
)x=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com