
ЁОЬтФПЁПСтаЮABCDжаЁЂЁЯBADЃН120ЁуЃЌЕуOЮЊЩфЯпCA ЩЯЕФЖЏЕуЃЌзїЩфЯпOMгыжБЯпBCЯрНЛгкЕуEЃЌНЋЩфЯпOMШЦЕуOФцЪБеыа§зЊ60ЁуЃЌЕУЕНЩфЯпONЃЌЩфЯпONгыжБЯпCDЯрНЛгкЕуFЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌЕуOгыЕуAжиКЯЪБЃЌЕуEЃЌFЗжБ№дкЯпЖЮBCЃЌCDЩЯЃЌЧыжБНгаДГіCEЃЌCFЃЌCAШ§ЬѕЖЮЖЮжЎМфЕФЪ§СПЙиЯЕЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌЕуOдкCAЕФбгГЄЯпЩЯЃЌЧвOAЃН![]() ACЃЌEЃЌFЗжБ№дкЯпЖЮBCЕФбгГЄЯпКЭЯпЖЮCDЕФбгГЄЯпЩЯЃЌЧыаДГіCEЃЌCFЃЌCAШ§ЬѕЯпЖЮжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ACЃЌEЃЌFЗжБ№дкЯпЖЮBCЕФбгГЄЯпКЭЯпЖЮCDЕФбгГЄЯпЩЯЃЌЧыаДГіCEЃЌCFЃЌCAШ§ЬѕЯпЖЮжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕуOдкЯпЖЮACЩЯЃЌШєABЃН6ЃЌBOЃН2![]() ЃЌЕБCFЃН1ЪБЃЌЧыжБНгаДГіBEЕФГЄЃЎ
ЃЌЕБCFЃН1ЪБЃЌЧыжБНгаДГіBEЕФГЄЃЎ

ЁОД№АИЁПЃЈ1ЃЉCA=CE+CFЃЎЃЈ2ЃЉCF-CE=![]() ACЃЎЃЈ3ЃЉBEЕФжЕЮЊ3Лђ5Лђ1ЃЎ
ACЃЎЃЈ3ЃЉBEЕФжЕЮЊ3Лђ5Лђ1ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМЂйжаЃЌНсТлЃКCA=CE+CFЃЎжЛвЊжЄУїЁїADFЁеЁїACEЃЈSASЃЉМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉНсТлЃКCF-CE=![]() ACЃЎШчЭМЂкжаЃЌШчЭМзїOGЁЮADНЛCFгкGЃЌдђЁїOGCЪЧЕШБпШ§НЧаЮЃЎжЛвЊжЄУїЁїFOGЁеЁїEOCЃЈASAЃЉМДПЩНтОіЮЪЬтЃЛ
ACЃЎШчЭМЂкжаЃЌШчЭМзїOGЁЮADНЛCFгкGЃЌдђЁїOGCЪЧЕШБпШ§НЧаЮЃЎжЛвЊжЄУїЁїFOGЁеЁїEOCЃЈASAЃЉМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЗжЫФжжЧщаЮЛГіЭМаЮЗжБ№ЧѓНтМДПЩНтОіЮЪЬт.
ЃЈ1ЃЉШчЭМЂйжаЃЌНсТлЃКCA=CE+CFЃЎ
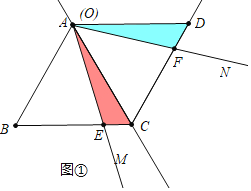
РэгЩЃКЁпЫФБпаЮABCDЪЧСтаЮЃЌЁЯBAD=120Ёу
ЁрAB=AD=DC=BCЃЌЁЯBAC=ЁЯDAC=60Ёу
ЁрЁїABCЃЌЁїACDЖМЪЧЕШБпШ§НЧаЮЃЌ
ЁпЁЯDAC=ЁЯEAF=60ЁуЃЌ
ЁрЁЯDAF=ЁЯCAEЃЌ
ЁпCA=ADЃЌЁЯD=ЁЯACE=60ЁуЃЌ
ЁрЁїADFЁеЁїACEЃЈSASЃЉЃЌ
ЁрDF=CEЃЌ
ЁрCE+CF=CF+DF=CD=ACЃЌ
ЁрCA=CE+CFЃЎ
ЃЈ2ЃЉНсТлЃКCF-CE=![]() ACЃЎ
ACЃЎ
РэгЩЃКШчЭМЂкжаЃЌШчЭМзїOGЁЮADНЛCFгкGЃЌдђЁїOGCЪЧЕШБпШ§НЧаЮЃЎ

ЁпЁЯGOC=ЁЯFOE=60ЁуЃЌ
ЁрЁЯFOG=ЁЯEOCЃЌ
ЁпOG=OCЃЌЁЯOGF=ЁЯACE=120ЁуЃЌ
ЁрЁїFOGЁеЁїEOCЃЈASAЃЉЃЌ
ЁрCE=FGЃЌ
ЁпOC=OGЃЌCA=CDЃЌ
ЁрOA=DGЃЌ
ЁрCF-EC=CF-FG=CG=CD+DG=AC+![]() AC=
AC=![]() ACЃЌ
ACЃЌ
ЃЈ3ЃЉзїBHЁЭACгкHЃЎЁпAB=6ЃЌAH=CH=3ЃЌ
ЁрBH=3![]() ЃЌ
ЃЌ
ШчЭМЂл-1жаЃЌЕБЕуOдкЯпЖЮAHЩЯЃЌЕуFдкЯпЖЮCDЩЯЃЌЕуEдкЯпЖЮBCЩЯЪБЃЎ
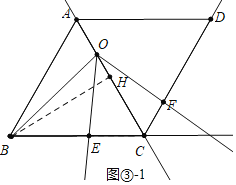
ЁпOB=2![]() ЃЌ
ЃЌ
ЁрOH=![]() =1ЃЌ
=1ЃЌ
ЁрOC=3+1=4ЃЌ
гЩЃЈ1ЃЉПЩжЊЃКCO=CE+CFЃЌ
ЁпOC=4ЃЌCF=1ЃЌ
ЁрCE=3ЃЌ
ЁрBE=6-3=3ЃЎ
ШчЭМЂл-2жаЃЌЕБЕуOдкЯпЖЮAHЩЯЃЌЕуFдкЯпЖЮDCЕФбгГЄЯпЩЯЃЌЕуEдкЯпЖЮBCЩЯЪБЃЎ
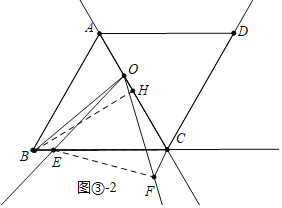
гЩЃЈ2ЃЉПЩжЊЃКCE-CF=OCЃЌ
ЁрCE=4+1=5ЃЌ
ЁрBE=1ЃЎ
ШчЭМЂл-3жаЃЌЕБЕуOдкЯпЖЮCHЩЯЃЌЕуFдкЯпЖЮCDЩЯЃЌЕуEдкЯпЖЮBCЩЯЪБЃЎ
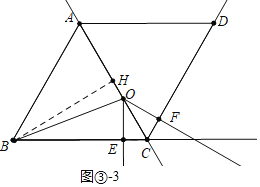
ЭЌЗЈПЩжЄЃКOC=CE+CFЃЌ
ЁпOC=CH-OH=3-1=2ЃЌCF=1ЃЌ
ЁрCE=1ЃЌ
ЁрBE=6-1=5ЃЎ
ШчЭМЂл-4жаЃЌЕБЕуOдкЯпЖЮCHЩЯЃЌЕуFдкЯпЖЮDCЕФбгГЄЯпЩЯЃЌЕуEдкЯпЖЮBCЩЯЪБЃЎ

ЭЌЗЈПЩжЊЃКCE-CF=OCЃЌ
ЁрCE=2+1=3ЃЌ
ЁрBE=3ЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФBEЕФжЕЮЊ3Лђ5Лђ1ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌАбвЛеХГЄЗНаЮПЈЦЌABCDЗХдкУПИёПэЖШЮЊ12mmЕФКсИёжНжаЃЌЧЁКУЫФИіЖЅЕуЖМдкКсИёЯпЩЯЃЌвбжЊЁЯІС=36ЁуЃЌЧѓГЄЗНаЮПЈЦЌЕФжмГЄЃЎЃЈОЋШЗЕН1mmЃЉЃЈВЮПМЪ§ОнЃКsin36ЁуЁж0.60ЃЌcos36ЁуЁж0.80ЃЌtan36ЁуЁж0.75ЃЉ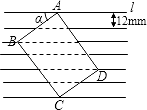
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAEЦНЗжЁЯBACЃЌBEЁЭAEгкЕуEЃЌЕуFЪЧBCЕФжаЕуЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌBEЕФбгГЄЯпгыACБпЯрНЛгкЕуDЃЌЧѓжЄЃКEF=![]() ЃЈACЉABЃЉЃЛ
ЃЈACЉABЃЉЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЧыжБНгаДГіЯпЖЮABЁЂACЁЂEFжЎМфЕФЪ§СПЙиЯЕЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋБпГЄЮЊ4ЕФе§ЗНаЮжНЦЌABCDелЕўЃЌЪЙЕУЕуAТфдкБпCDЕФжаЕуEДІЃЌелКлЮЊFGЃЌЕуFЁЂGЗжБ№дкБпADЁЂBCЩЯЃЌдђелКлFGЕФГЄЖШЮЊ_____.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпCЃКy=x2Љ2x+1ЕФЖЅЕуЮЊPЃЌгыyжсЕФНЛЕуЮЊQЃЌЕуFЃЈ1ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ1ЃЉЧѓtanЁЯOPQЕФжЕЃЛ
ЃЈ2ЃЉНЋХзЮяЯпCЯђЩЯЦНвЦЕУЕНХзЮяЯпCЁфЃЌЕуQЦНвЦКѓЕФЖдгІЕуЮЊQЁфЃЌЧвFQЁф=OQЁфЃЎ
ЂйЧѓХзЮяЯпCЁфЕФНтЮіЪНЃЛ
ЂкШєЕуPЙигкжБЯпQЁфFЕФЖдГЦЕуЮЊKЃЌЩфЯпFKгыХзЮяЯпCЁфЯрНЛгкЕуAЃЌЧѓЕуAЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЕШБпШ§НЧаЮABCЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊAЃЈ0ЃЌ0ЃЉЁЂBЃЈ6ЃЌ0ЃЉЃЌЗДБШР§КЏЪ§ЕФЭМЯѓОЙ§ЕуCЃЎ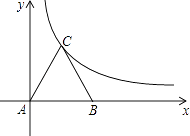
ЃЈ1ЃЉЧѓЕуCЕФзјБъМАЗДБШР§КЏЪ§ЕФНтЮіЪНЃЎ
ЃЈ2ЃЉНЋЕШБпЁїABCЯђЩЯЦНвЦnИіЕЅЮЛЃЌЪЙЕуBЧЁКУТфдкЫЋЧњЯпЩЯЃЌЧѓnЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌCA=CBЃЌдкЁїAEDжаЃЌDA=DEЃЌЕуDЃЌEЗжБ№дкCAЃЌABЩЯЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌШєЁЯACB=ЁЯADE=90ЁуЃЌдђCDгыBEЕФЪ§СПЙиЯЕЪЧЃЛ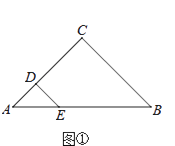
ЃЈ2ЃЉШєЁЯACB=ЁЯADE=120ЁуЃЌНЋЁїAEDШЦЕуAа§зЊжСШчЭМЂкЫљЪОЕФЮЛжУЃЌдђCDгыBEЕФЪ§СПЙиЯЕЪЧЃЛЃЌ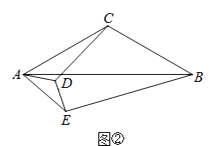
ЃЈ3ЃЉШєЁЯACB=ЁЯADE=2ІСЃЈ0ЁуЃМІСЃМ90ЁуЃЉЃЌНЋЁїAEDШЦЕуAа§зЊжСШчЭМЂлЫљЪОЕФЮЛжУЃЌЬНОПЯпЖЮCDгыBEЕФЪ§СПЙиЯЕЃЌВЂМгвджЄУїЃЈгУКЌІСЕФЪНзгБэЪОЃЉЃЎ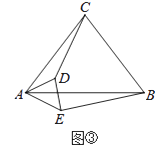
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
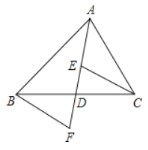
ЁОЬтФПЁПШчЭМЃЌ ![]() ЪЧ
ЪЧ![]() ЕФжаЯпЃЌ
ЕФжаЯпЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() КЭ
КЭ![]() бгГЄЯпЩЯЕФЕуЃЌЧв
бгГЄЯпЩЯЕФЕуЃЌЧв![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌ
ЃЌ![]() ЃЎЯТСаЫЕЗЈЃКЂй
ЃЎЯТСаЫЕЗЈЃКЂй![]() ЃЛЂк
ЃЛЂк![]() КЭ
КЭ![]() УцЛ§ЯрЕШЃЛЂл
УцЛ§ЯрЕШЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЎЦфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ
ЃЎЦфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ
A.![]() ИіB.
ИіB.![]() ИіC.
ИіC.![]() ИіD.
ИіD.![]() Иі
Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBAC=60ЁуЃЌЁЯBACЕФЦНЗжЯпADгыБпBCЕФДЙжБЦНЗжЯпMDЯрНЛгкЕуDЃЌDEЁЭABНЛABЕФбгГЄЯпгкЕуEЃЌDFЁЭACгкЕуFЃЌЯжгаЯТСаНсТлЃКЂйDE=DFЃЛЂкDE+DF=ADЃЛЂлDMЦНЗжЁЯADFЃЛЂмAB+AC=2AE.ЦфжаЃЌе§ШЗЕФгаЃЈ ЃЉ
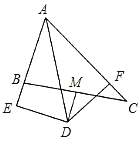
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com