
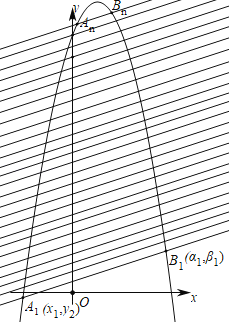
【题目】已知二次函数y=﹣x2+5x+2019,有一组平行直线与该函数的相交情况如下:
y1=2x+1与之交于A1(x1,y1)、B1(α1,β1),
y2=2x+2与之交于A2(x2,y2)、B1(α2,β2),
y3=2x+3与之交于A1(x3,y3)、B1(α3,β3),
……
yn=2x+n与之交于An(xn,yn)、Bn(αn,βn),
(1)求x1+α1与x2+α2的值;
(2)求整数n的最大值;
(3)求(x1+x1+x3+…+xn)+(α1+α2+α3+.…+αn)的值.
【答案】(1)x1+α1=3,x2+α2=3;(2)2021;(3)3n.
【解析】
(1)将二次函数与一次函数的解析式联立方程,再由一元二次方程的根与系数的关系解答即可;
(2)当y=2x+n与抛物线y=﹣x2+5x+2019有一个交点时,此时n最大,利用△=0即可求解;
(3)先将所求式子转化为(x1+a1)+(x2+α2)+…+(xn+αn),再结合(1)题的结论即可求解.
解:(1)由题意可得2x+1=﹣x2+5x+2019,即x2-3x-2018=0,
∵x1、α1是上述方程的两个根,∴x1+α1=3;
同理2x+2=﹣x2+5x+2019,即x2-3x-2017=0,
∵x2、α2是上述方程的两个根,∴x2+α2=3;
(2)2x+n=﹣x2+5x+2019,即x2﹣3x+n﹣2019=0,
当△=0时,可得9﹣4n+8076=0,解得:n=2021.25,
∵n为整数,∴n的最大值是2021;
(3)由(1)得:x1+α1=3,x2+α2=3,…,xn+αn=3;
∴(x1+x1+x3+…+xn)+(α1+α2+α3+…+αn)=(x1+a1)+(x2+α2)+…+(xn+αn)=3n.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】欢欢放学回家看到桌上有三个礼包,是爸爸送给欢欢和姐姐的礼物,其中![]() 礼包是芭比娃娃,
礼包是芭比娃娃,![]() 和
和![]() 礼包都是智能对话机器人.这些礼包用外表一样的包装盒装着,看不到里面的礼物.
礼包都是智能对话机器人.这些礼包用外表一样的包装盒装着,看不到里面的礼物.
(1)欢欢随机地从桌上取出一个礼包,取出的是芭比娃娃的概率是多少?
(2)请用树状图或列表法表示欢欢随机地从桌上取出两个礼包的所有可能结果,并求取出的两个礼包都是智能对话机器人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
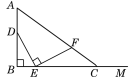
【题目】如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE=![]() DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式为( )
DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式为( )
A.-![]() B.-
B.-![]() C.-
C.-![]() D.-
D.-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
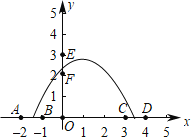
【题目】如图,在一个与地面垂直的截面中建立直角坐标系(横坐标表示地面位移,纵坐标表示高度),一架无人机的飞行路线为y=ax2+bx+c(a≠0),在直角坐标系中x轴上的线段AB上的某点起飞,途经空中线段EF上的某点,最后在线段CD上的某点降落,其中A(﹣2,0)、B(﹣1,0)、C(3,0)、D(4,0)、E(0,3)、F(0,2),则下列结论正确的有_____(填序号)
(1)abc<0;
(2)从起飞到当x≤1时无人机一直是上升的;
(3)2≤a+b+c≤4.5;
(4)最大飞行高度不超过4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③方程ax2+bx+c=0的两根分别为﹣3和1;④当x<1时,y<0.其中正确的命题是( )
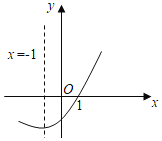
A.②③B.①③C.①②D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为5,D、E分别是边AB、AC上的点,将△ADE沿DE折叠,点A恰好落在BC边上的点F处,若BF=2,则BD的长是( )
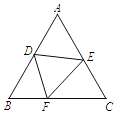
A.2B.3C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
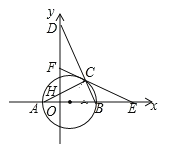
【题目】如图,在平面直角坐标系中,△ABC内接于⊙P,AB是⊙P的直径,A(﹣1,0)、C(3,2![]() ),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.
),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.
(1)求⊙P的半径;
(2)当∠A=∠DCF时,求证:CE是⊙P的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com