
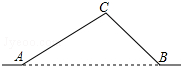
 如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)分析 作CH⊥AB于H.在Rt△ACH中根据CH=AC•sin∠CAB求出CH的长,由AH=AC•cos∠CAB求出AH的长,同理可得出BH的长,根据AB=AH+BH可得出结论;
解答 解:如图,过点C作CD⊥AB于点D. 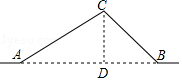
在Rt△ACD中,∠ADC=90°,sin34°=$\frac{CD}{AC}$,cos34°=$\frac{AD}{AC}$.
∴CD≈10×0.559=5.59,AD≈10×0.675=6.75.
∵∠ABC=45°,∴BD=CD=5.59.
∴AB=AD+BD=6.75+5.59≈12.3(千米).
答:改直后的公路AB的长约为12.3千米.
点评 本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
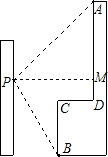 小明在教学楼的点P处观测对面的实验楼,为了测量坐在位置点P到对面实验楼上部AD的距离,小强测得实验楼楼顶部点A的仰角为45°,测得实验楼底部点B的俯角为60°,已知实验楼高30米,CD=10米.求点P到AD的距离(结果保留到0.1米)
小明在教学楼的点P处观测对面的实验楼,为了测量坐在位置点P到对面实验楼上部AD的距离,小强测得实验楼楼顶部点A的仰角为45°,测得实验楼底部点B的俯角为60°,已知实验楼高30米,CD=10米.求点P到AD的距离(结果保留到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com