
【题目】为创建国家级文明卫生城市,搞好“大美伊春,天然氧吧”的宣传活动,我市园林部门计划用不超过2950盆甲种花卉和2470盆乙种花卉,组建中、小型两类盆景50个.已知组建一个中型盆景需甲种花卉75盆,乙种花卉45盆;组建一个小型盆景需甲种花卉35盆,乙种花卉55盆.
(1)问符合题意的组建方案有几种?请你帮园林部门设计出来;
(2)若组建一个中型盆景的费用是920元,组建一个小型盆景的费用是630元,试说明在(1)中哪种方案费用最低?最低费用是多少元?
【答案】(1)有三种组建方案:方案一,组建中型盆景28个,小型盆景22个;方案二,组建中型盆景29个,小型盆景21个;方案三,组建中型盆景30个,小型盆景20个;(2)选择方案1时费用最低为39620元.
【解析】
根据题意设组建中型盆景x个,则小型盆景(50-x)个,由题意可列出一元一次不等式组,解出不等式的解集再根据实际情况即可得方案;因为中型盆景价格比小型盆景贵,所以中型盆景越少,价格越低,由此可知最低费用.
解:设组建中型盆景x个,则小型盆景(50-x)个,
由题意可列![]() ,
,
解得![]() ,即
,即![]() ,
,
由于要取整数,故x=28,29,30,
故有三种方案:方案一,组建中型盆景28个,小型盆景22个;
方案二,组建中型盆景29个,小型盆景21个;
方案三,组建中型盆景30个,小型盆景20个;
(2)∵组建一个中型盆景的费用比小型盆景贵,
∴中型盆景越少,价格越低
∴最低费用为第一种方案,即28![]() 920+22
920+22![]() 630=39620(元)
630=39620(元)


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=30°,点D是△ABC内一点,DB=DC,∠DCB=30°,点E是BD延长线上一点,AE=AB.
(1)求∠ADE的度数;
(2)求证:DE=AD+DC;
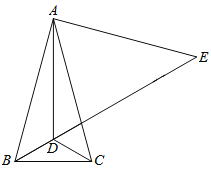
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是( )
A.红红不是胜就是输,所以红红胜的概率为 ![]()
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为 ![]()
D.娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,元旦期间,小明乘汽车从![]() 地出发,经过
地出发,经过![]() 地到目的地
地到目的地![]() 地(三地在同一条直线上),假设汽车从
地(三地在同一条直线上),假设汽车从![]() 到
到![]() 的过程都是匀速直线行驶.图2表示小明离
的过程都是匀速直线行驶.图2表示小明离![]() 地的路程
地的路程![]() (km)与汽车从
(km)与汽车从![]() 出发后行驶时间
出发后行驶时间![]() (h)之何的函数关系图象.
(h)之何的函数关系图象.
(1) ![]() 两地间的路程为 km;
两地间的路程为 km;
(2)求小明离![]() 地的路程
地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(3)当行驶时间![]() 在什么范围时,汽车离
在什么范围时,汽车离![]() 地的路程不超过40 km?
地的路程不超过40 km?
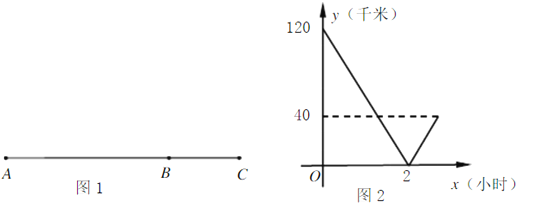
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完;销售金额与卖西瓜千克数之间的关系如图所示,那么小李赚了_________.元.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中建立平面直角坐标系后,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ;
;
(2)借助图中的网格,请只用直尺(不含刻度)完成以下要求:(友情提醒:请别忘了标注字母)
①在图中找一点![]() ,使得
,使得![]() 到边
到边![]() 的距离相等,且
的距离相等,且![]() ;
;
②在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 的周长最小,并求出此时点
的周长最小,并求出此时点![]() 的坐标.
的坐标.
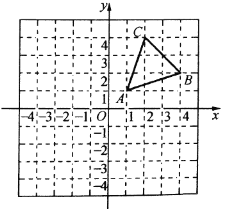
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,已知点
中,已知点 ![]() ,
, ![]() .若平移点
.若平移点 ![]() 到点
到点 ![]() ,使以点
,使以点 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的四边形是菱形,则正确的平移方法是( )
为顶点的四边形是菱形,则正确的平移方法是( )
A.向左平移1个单位,再向下平移1个单位
B.向左平移 ![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
C.向右平移 ![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
D.向右平移1个单位,再向上平移1个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(-1,5),B(4,2),C(-1,0)三点.
(1)点A的对称点A′的坐标为(1,-5),点B关于x轴的对称点B′的坐标为________,点C关于y轴的对称点C′的坐标为________;
(2)求(1)中的△A′B′C′的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com