
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() (
(![]() )与双曲线
)与双曲线![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在第一象限),直线
在第一象限),直线![]() (
(![]() )与双曲线
)与双曲线![]() 交于
交于![]() ,
,![]() 两点.当这两条直线互相垂直,且四边形
两点.当这两条直线互相垂直,且四边形![]() 的周长为
的周长为![]() 时,点
时,点![]() 的坐标为_________.
的坐标为_________.
【答案】![]() 或
或![]()
【解析】
首先根据题意求出点A坐标为(![]() ,
,![]() ),从而得出
),从而得出![]() ,然后分两种情况:①当点B在第二象限时求出点B坐标为(
,然后分两种情况:①当点B在第二象限时求出点B坐标为(![]() ,
,![]() ),从而得出
),从而得出![]() ,由此可知
,由此可知![]() ,再利用平面直角坐标系任意两点之间的距离公式可知:
,再利用平面直角坐标系任意两点之间的距离公式可知:![]() ,所以
,所以![]() ,据此求出
,据此求出![]() ,由此进一步通过证明四边形ABCD是菱形加以分析求解即可得出答案;②当点B在第四象限时,方法与前者一样,具体加以分析即可.
,由此进一步通过证明四边形ABCD是菱形加以分析求解即可得出答案;②当点B在第四象限时,方法与前者一样,具体加以分析即可.
∵直线![]() (
(![]() )与双曲线
)与双曲线![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在第一象限),
在第一象限),
∴联立二者解析式可得: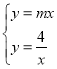 ,由此得出点A坐标为(
,由此得出点A坐标为(![]() ,
,![]() ),
),
∴![]() ,
,
①当点B在第二象限时,如图所示:
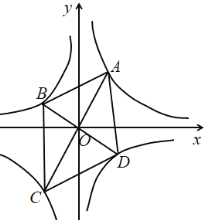
∵直线![]() (
(![]() )与双曲线
)与双曲线![]() 交于
交于![]() ,
,![]() 两点,
两点,
∴联立二者解析式可得: ,由此得出点B坐标为(
,由此得出点B坐标为(![]() ,
,![]() ),
),
∴![]() ,
,
∵AC⊥BD,
∴![]() ,
,
根据平面直角坐标系任意两点之间的距离公式可知:
![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ,
,
根据反比例函数图象的对称性可知:OC=OA,OB=OD,
∵AC⊥BD,
∴四边形ABCD是菱形,
∴![]() ,
,
∴![]() ,
,
解得:![]() 或2,
或2,
∴A点坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),
),
②当点B在第四象限时,如图所示:
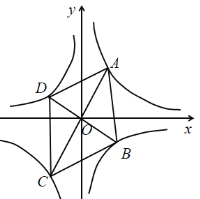
∵直线![]() (
(![]() )与双曲线
)与双曲线![]() 交于
交于![]() ,
,![]() 两点,
两点,
∴联立二者解析式可得: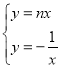 ,由此得出点B坐标为(
,由此得出点B坐标为(![]() ,
,![]() ),
),
∴![]() ,
,
∵AC⊥BD,
∴![]() ,
,
根据平面直角坐标系任意两点之间的距离公式可知:
![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ,
,
根据反比例函数图象的对称性可知:OC=OA,OB=OD,
∵AC⊥BD,
∴四边形ABCD是菱形,
∴![]() ,
,
∴![]() ,
,
解得:![]() 或2,
或2,
∴A点坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),
),
综上所述,点A坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),
),
故答案为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,∠BCD=90°,BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.
(1)判断:∠ABC ∠PDC(填“>”或“=”或“<”);
(2)猜想△ACE的形状,并说明理由;
(3)若△ABC的外心在其内部(不含边界),直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本校九年级学生体育测试项目“400米跑”的训练情况,体育教师在2019年1-5月份期间,每月随机抽取部分学生进行测试,将测试成绩分为:A,B,C,D四个等级,并绘制如下两幅统计图.根据统计图提供的信息解答下列问题:

(1)______月份测试的学生人数最少,______月份测试的学生中男生、女生人数相等;
(2)求扇形统计图中D等级人数占5月份测试人数的百分比;
(3)若该校2019年5月份九年级在校学生有600名,请你估计出测试成绩是A等级的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将函数![]() 为常数)的图象记为
为常数)的图象记为![]() 图象
图象![]() 与直线
与直线![]() 的交点坐标为
的交点坐标为![]() .
.
(1)若点![]() 在图象
在图象![]() 上,求
上,求![]() 的值;
的值;
(2)求![]() 的最小值;
的最小值;
(3)当直线![]() 的图象与函数
的图象与函数![]() 为常数)的图像只有一个公共点时,求
为常数)的图像只有一个公共点时,求![]() 的取值范围;
的取值范围;
(4)若![]() 点
点![]() 在图象
在图象![]() 上,且点
上,且点![]() 的横坐标为
的横坐标为![]() 点
点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() .当点
.当点![]() 不在坐标轴上时,以点
不在坐标轴上时,以点![]() 为顶点构造矩形
为顶点构造矩形![]() 使点
使点![]() 落在
落在![]() 轴上.当图象
轴上.当图象![]() 与矩形
与矩形![]() 的边有两个公共点时,直接写出
的边有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象过点A(-2,0),B(4,0),C(0,4)
(1)求二次函数的解析式;
(2)如图,当点P为AC的中点时,在线段PB上是否存在点M,使得∠BMC=90°?若存在,求出点M的坐标,若不存在,请说明理由.
(3)点K在抛物线上,点D为AB的中点,直线KD与直线BC的夹角为锐角![]() ,且tan
,且tan![]() =
=![]() ,求点K的坐标.
,求点K的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国魏晋时期著名的数学家刘徽在《九章算术》中提出了“割圆术——割之弥细,所失弥少,隔之又割,以至不可割,则与圆周合体,而无所失也.”也就是利用圆的内接多边形逐步逼近圆的方法来近似计算圆的面积和周长.如图1,若用圆的内接正六边形的面积![]() 来近似估计半径为1的⊙O的面积,再用如图2的圆的内接正十二边形的面积
来近似估计半径为1的⊙O的面积,再用如图2的圆的内接正十二边形的面积![]() 来近似估计半径为1的⊙O的面积,则
来近似估计半径为1的⊙O的面积,则![]() ____.(结果保留根号)
____.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知轮船甲在A处沿北偏东65°的方向匀速航行,同时轮船乙在轮船甲的南偏东40°方向的点B处沿某一方向航行,速度与甲轮船的速度相同.若经过一段时间后,两艘轮船恰好相遇,则轮船乙的航行方向为( )
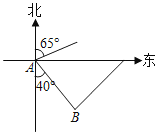
A.北偏西40°B.北偏东40°C.北偏西35°D.北偏东35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片![]() 沿过点
沿过点![]() 的直线折叠,使得点
的直线折叠,使得点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ;再将
;再将![]() 分别沿
分别沿![]() 折叠,此时点
折叠,此时点![]() 落在
落在![]() 上的同一点
上的同一点![]() 处.请完成下列探究:
处.请完成下列探究:
![]() 的大小为__________
的大小为__________![]() ;
;
![]() 当四边形
当四边形![]() 是平行四边形时
是平行四边形时![]() 的值为__________.
的值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,AC=BC,点P在线段BA的延长线上,作PD⊥AC,交AC的延长线于点D,点D关于直线AB的对称点为E,连接PE并延长PE到点F,使EF=AC,连接CF.
(1)依题意补全图1;
(2)求证:AD=CF;
(3)若AC=2,点Q在直线AB上,写出一个AQ的值,使得对于任意的点P总有QD=QF,并证明.
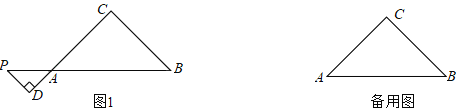
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com