Question

14．图中是小明设计的带正方形图案的花边作品，该作品由形如图乙的矩形图案及轴对称图形拼接而成（不重叠，无缝隙），图乙中，点E，F分别是矩形ABCD的边AD、BC的中点，两条平行线AL，CK分别经过正方形顶点H，G和正方形的边EG，FH的中点P，Q，测得PG=2cm，则图乙中两个阴影四边形的面积之和为$\frac{40}{3}$cm²．

Answer 1

分析 如图，连接HC、EF、GH，EF分别与GH、AL交于O、N．首先证明四边形ABFE，四边形EFCD是正方形，由△EHN≌△CHL，推出S_△CHL=S_△ENH，由HO∥AE，推出$\frac{OH}{AE}$=$\frac{ON}{NE}$=$\frac{1}{2}$，
推出OE=$\frac{3}{2}$EN，推出S_△ENH=$\frac{2}{3}$S_△EOH，求出△CHL，△CHQ的面积即可解决问题．

解答 解：如图，连接HC、EF、GH，EF分别与GH、AL交于O、N．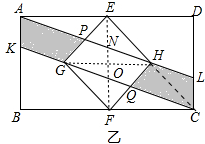

∵四边形ABCD是矩形，AE=ED，BF=FC，
∴AE∥BF，AE=BF，
∴四边形ABFE是平行四边形，∵∠B=90°，
∴四边形AEFB是矩形，同理四边形EFCD是矩形，
∵四边形EGFH是正方形，
∴GH⊥EF，
∴∠GOF=∠AEF=90°，
∴GH∥AE，
∴$\frac{AE}{GH}$=$\frac{PE}{PG}$=1，
∴AE=ED=GH=EF，
∴四边形ABFE，四边形EFCD是正方形，
∴∠FEH=∠EFH=∠HED=45°，
∴E、H、C共线，点H是正方形EDCF的对角线的交点，
∵EN∥CL，EH=CH，
∴$\frac{HN}{HL}$=$\frac{EH}{HC}$=$\frac{EN}{CL}$=1，
∴HN=HL，EN=CL，
∴△EHN≌△CHL，
∴S_△CHL=S_△ENH，
∵HO∥AE，
∴$\frac{OH}{AE}$=$\frac{ON}{NE}$=$\frac{1}{2}$，
∴OE=$\frac{3}{2}$EN，
∴S_△ENH=$\frac{2}{3}$S_△EOH，
根据对称性可知，AC=CQ=PH=GQ，FQ=QH，
∴S_△QCH=S_△GQH=$\frac{1}{2}$S_△GHF，
∵PG=PE=2，
∴EG=EH=4，
∴S_△EOH=$\frac{1}{4}$×4²=4，S_△GHF=$\frac{1}{2}$×4²=8，
∴S_△CHL+S_△CHQ=$\frac{2}{3}$×4+4=$\frac{20}{3}$，
∴S_阴=2×$\frac{20}{3}$=$\frac{40}{3}$．
故答案为$\frac{40}{3}$．

点评 本题科学图形的拼剪、对称轴设计图案、矩形、正方形的性质等知识，解题的关键是学会添加常用辅助线，构造特殊四边形解决问题，求出△CHL，△CHQ的面积是解题的突破口，属于中考常考题型．