
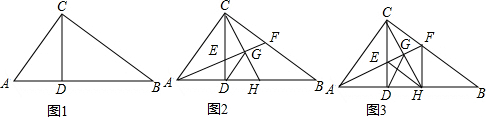
分析 (1)证明△ACD∽△ABC,利用相似三角形的性质即可期初答案.
(2)先根据AF平分∠CAB证明△CEF为等腰三角形,由三线合一定理可知CH⊥EF,从而可知A、D、G、C四点共圆,由圆周角定理即可求证∠AGD=∠B.
(3)当∠ABC=30°时,可证明四边形CEHF是菱形,从而可证明点E、H分别是AF、AB的中点,设S△CGF=S△CEG=S△EGH=S△GFH=x,从而可求出S△FHB=S△FHA=4x.
解答 证明:(1)∵∠A=∠A,∠ADC=∠ADB=90°,
∴△ACD∽△ABC,
∴$\frac{AC}{AD}=\frac{AB}{AC}$,
即AC2=AB•AD
(2)∵AF平分∠CAB,
∴∠CAF=∠DAE,
∵∠CAF+∠CFA=∠DAE+∠AED=90°,
∴∠CFA=∠AED,
∵∠CEF=∠AED,
∴∠CEF=∠CFA
∴△CEF为等腰三角形
∵G为EF的中点
∴CH⊥EF
又CD⊥AB
∴A、D、G、C四点共圆,
∴∠AGD=∠ACD,
∵∠ACD+∠DCB=∠DCB+∠B=90°,
∴∠ACD=∠B,
∴∠AGD=∠B
(3)当∠ABC=30°时,
∴∠ACD=∠ABC=30°,
∴∠DCB=∠AFH=60°
由(2)可知:CH垂直平分EF,
∴△CEF与△HEF是等腰直角三角形,
∴△CEF与△HEF是等边直角三角形,
∴四边形CEHF是菱形,
∴AE=CF=EF=CE,
∴E是AF的中点,
同理可证:H是AB的中点,
设S△CGF=S△CEG=S△EGH=S△GFH=x
则S△AEC=2x=S△AEH
∴S△FHB=S△FHA=4x
∴S四边形CEHF:S△ABC=1:3
点评 本题考查相似三角形综合问题,涉及圆周角定理,等腰三角形的性质与判定,相似三角形的性质与判定,需要学生灵活运用所学知识进行解答,题目较为综合.


科目:初中数学 来源: 题型:解答题
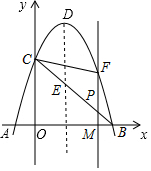 如图,抛物线y=-x2+2x+3与x轴相交于A、B两点,与y轴相交于点C,顶点为D.
如图,抛物线y=-x2+2x+3与x轴相交于A、B两点,与y轴相交于点C,顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
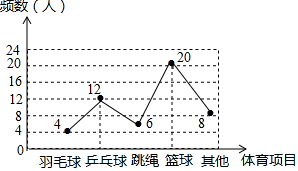 体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )
体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )| A. | 16% | B. | 24% | C. | 30% | D. | 40% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com